为了调查学生星期天晚上学习时间利用问题,某校从高二年级1000名学生(其中走读生450名,住宿生550名)中,采用分层抽样的方法抽取 名学生进行问卷调查,根据问卷取得了这
名学生进行问卷调查,根据问卷取得了这 名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组①
名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组① ,②
,② ,③
,③ ,④
,④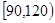 ,⑤
,⑤ ,⑥
,⑥ ,⑦
,⑦ ,⑧
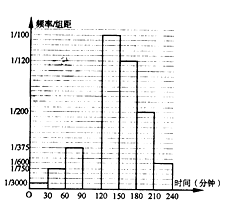
,⑧ ,得到频率分布直方图如下,已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人:
,得到频率分布直方图如下,已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人:
(1)求 的值并补全下列频率分布直方图;
的值并补全下列频率分布直方图;
(2)如果把“学生晚上学习时间达到两小时”作为是否充分利用时间的标准,对抽取的 名学生,完成下列
名学生,完成下列 列联表:
列联表:
| 利用时间充分 |
利用时间不充分 |
总计 |
|
| 走读生 |
|||
| 住宿生 |
10 |
||
| 总计 |
据此资料,你是否认为学生“利用时间是否充分”与走读、住宿有关?
参考公式:
如图,多面体 中,
中,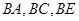 两两垂直,且
两两垂直,且 ,
,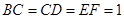 .
.
(1)若点 在线段
在线段 上,且
上,且 ,求证:
,求证: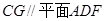 ;
;
(2)求多面体 的体积.
的体积.
已知抛物线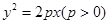 的焦点为
的焦点为 ,准线为
,准线为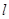 ,过点
,过点 的直线交抛物线于
的直线交抛物线于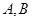 两点,过点
两点,过点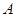 作准线
作准线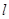 的垂线,垂足为
的垂线,垂足为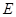 ,当
,当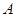 点的坐标为
点的坐标为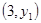 时,
时,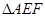 为正三角形,则此时
为正三角形,则此时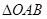 的面积为()
的面积为()
A.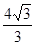 |
B.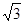 |
C.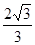 |
D.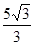 |
已知函数 ,则下列说法正确的为()
,则下列说法正确的为()
A.函数 的最小正周期为 的最小正周期为 |
B.函数 的最大值为 的最大值为 |
C.函数 的图象关于直线 的图象关于直线 对称 对称 |
D.将 图像向右平移 图像向右平移 个单位长度,再向下平移 个单位长度,再向下平移 个单位长度后会得到一个奇函数图像 个单位长度后会得到一个奇函数图像 |
选修4—5:不等式选讲.
设函数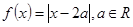 .
.
(1)若不等式 的解集为
的解集为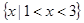 ,求
,求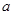 的值;
的值;
(2)若存在 ,使
,使 ,求
,求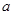 的取值范围.
的取值范围.