数列{an}的前n项和为Pn,若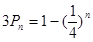 (n∈N*),数列{bn}满足2bn+1=bn+bn+2(n∈N*),且b3=7,b8=22.
(n∈N*),数列{bn}满足2bn+1=bn+bn+2(n∈N*),且b3=7,b8=22.
(1)求数列{an}和{bn}的通项公式an和bn;
(2)设数列cn=anbn,求{cn}的前n项和Sn.
已知函数 .
.
(Ⅰ)求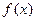 的最小正周期;
的最小正周期;
(Ⅱ)若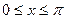 ,求
,求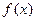 的单调区间.
的单调区间.
已知数列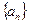 是公差不为零的等差数列,
是公差不为零的等差数列,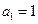 且
且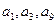 成等比数列.
成等比数列.
(Ⅰ)求数列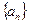 的通项公式;
的通项公式;
(Ⅱ)若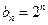 ,求数列
,求数列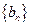 的前n项和.
的前n项和.
函数 的图象与函数
的图象与函数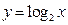 的图象交于两点
的图象交于两点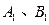 (
(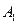 在线段
在线段 上,
上, 为坐标原点),过
为坐标原点),过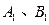 作
作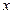 轴的垂线,垂足分别为
轴的垂线,垂足分别为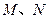 ,并且
,并且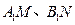 分别交函数
分别交函数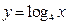 的图象于
的图象于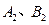 两点.
两点.
(1)试探究线段 的大小关系;
的大小关系;
(2)若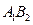 平行于
平行于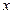 轴,求四边形
轴,求四边形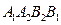 的面积.
的面积.
(本小题满分16分)
如图,多面体 中,
中, 两两垂直,平面
两两垂直,平面 平面
平面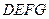 ,
,
平面 平面
平面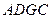 ,
,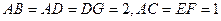 .
.
(1)证明四边形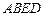 是正方形;
是正方形;
(2)判断点 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?
(3)连结 ,求证:
,求证: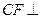 平面
平面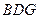 .
.
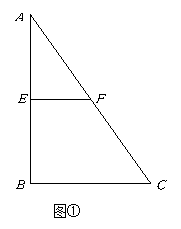
(本小题满分16分)如图①,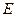 ,
, 分别是直角三角形
分别是直角三角形 边
边 和
和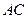 的中点,
的中点,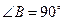 ,沿
,沿 将三角形
将三角形 折成如图②所示的锐二面角
折成如图②所示的锐二面角 ,若
,若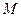 为线段
为线段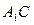 中点.求证:
中点.求证:
(1)直线 平面
平面 ;
;
(2)平面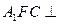 平面
平面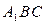 .
.