如图,已知反比例函数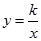 与一次函数
与一次函数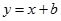 的图象在第一象限相交于点A(1,
的图象在第一象限相交于点A(1, )
)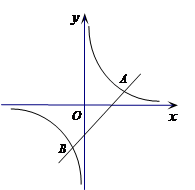
(1)试确定这两个函数的表达式;
(2)求出这两个函数图像的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
如图, 点 , , 都在抛物线 (其 中 上, 轴, ,且 .
(1) 填空: 抛物线的顶点坐标为 (用 含 的代数式表示) ;
(2) 求 的面积 (用 含 的代数式表示) ;
(3) 若 的面积为 2 ,当 时, 的最大值为 2 ,求 的值 .

阅读下面材料:
小明遇到这样一个问题:
如图1, 中, ,点 在 上,且 ,求证: .
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作 平分 ,与 相交于点 .
方法2:如图3,作 ,与 相交于点 .
(1)根据阅读材料,任选一种方法,证明 .
用学过的知识或参考小明的方法,解决下面的问题:
(2)如图4, 中,点 在 上,点 在 上,且 ,点 在 上,且 ,延长 、 ,相交于点 ,且 .
①在图中找出与 相等的角,并加以证明;
②若 ,猜想线段 与 的数量关系,并证明你的猜想.

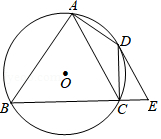
如图,四边形 内接于 , ,点 在 的延长线上,且 .
(1)求证: 是 的切线;
(2)若 ,当 , 时,求 的长.
【观察】 , , , , , , , , , , , , .
【发现】根据你的阅读回答问题:
(1)上述内容中,两数相乘,积的最大值为 ;
(2)设参与上述运算的第一个因数为 ,第二个因数为 ,用等式表示 与 的数量关系是 .
【类比】观察下列两数的积: , , , , , , , , , , .
猜想 的最大值为 ,并用你学过的知识加以证明.
甲、乙两名学生练习打字,甲打135个字所用时间与乙打180个字所用时间相同.已知甲平均每分钟比乙少打20个字,求甲平均每分钟打字的个数.