如图1,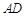 是直角△
是直角△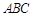 斜边上的高,沿
斜边上的高,沿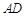 把△
把△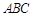 的两部分折成直二面角(如图2),
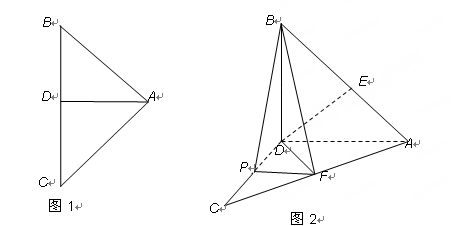
的两部分折成直二面角(如图2),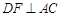 于
于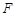 .
.
(Ⅰ)证明: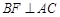 ;
;
(Ⅱ)设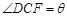 ,
,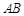 与平面
与平面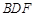 所成的角为
所成的角为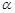 ,二面角
,二面角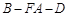 的大小为
的大小为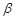 ,试用
,试用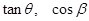 表示
表示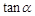 ;
;
(Ⅲ)设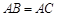 ,
,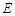 为
为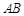 的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点 ,使得
,使得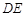 ∥平面
∥平面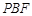 ? 若存在,求
? 若存在,求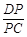 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分14分)
已知二项式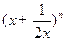 (n∈N* , n≥2).
(n∈N* , n≥2).
(1)若该二项式的展开式中前三项的系数成等差数列,求正整数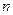 的值;
的值;
(2)在(1)的条件下,求展开式中x4项的系数.
(本小题满分14分)
如图,在几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA⊥AB,M是EC的中点,EA=DA=AB=2CB.
(1)求证:DM⊥EB; (2)求异面直线AB与CE所成角的余弦值.
 |
(本题16分)如图,某大风车的半径为2米,每12秒沿逆时针方向旋转一周,它的最底点 离地面1米,风车圆周上一点A从最底点
离地面1米,风车圆周上一点A从最底点 开始,运动t秒后与地面距离为h米,
开始,运动t秒后与地面距离为h米,
(1)求函数h=f(t)的关系式, 并在给出的方格纸上用五点作图法作出h=f(t)在一个周期内的图象(要列表,描点);
(2) A从最底点 开始, 沿逆时针方向旋转第一周内,有多长时间离地面的高度超过4米?
开始, 沿逆时针方向旋转第一周内,有多长时间离地面的高度超过4米?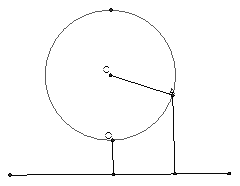
(本题16分)函数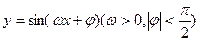 在同一个周期内,当
在同一个周期内,当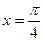 时
时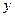 取最大值1,当
取最大值1,当 时,
时,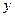 取最小值
取最小值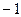 。
。
(1)求函数的解析式
(2)函数 的图象经过怎样的变换可得到
的图象经过怎样的变换可得到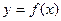 的图象?
的图象?
(3)若函数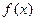 满足方程
满足方程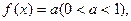 求在
求在 内的所有实数根之和.
内的所有实数根之和.
函数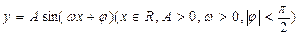 的图象上相邻的最高点与最低点的坐标分别为M(
的图象上相邻的最高点与最低点的坐标分别为M(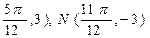 ,求此函数的解析式。
,求此函数的解析式。