如图,点P(0,−1)是椭圆C1: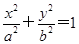 (a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.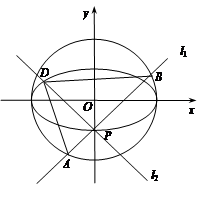
(Ⅰ)求椭圆C1的方程;
(Ⅱ)求△ABD面积取最大值时直线l1的方程.
已知条件 条件
条件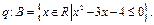 若
若 是
是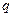 的充分但不必要条件,求实
的充分但不必要条件,求实 数
数 的取值范围.
的取值范围.
某种产品的广告费用支出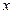 万元与销售额
万元与销售额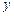 万元之间有如下的对应
万元之间有如下的对应 数据:
数据:
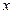 |
2 |
4 |
5 |
6 |
8 |
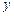 |
20 |
30 |
50 |
50 |
70 |
(1)画出上表数据的散点图;
(2)根据上表提供的数据, 求出y关于x的线性回归方程;
求出y关于x的线性回归方程;
(3)据此估计广告费用为10万元时,所得的销售收入.
(参考数值: 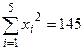 ,
, ,)
,)
(14)已知函数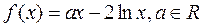
(Ⅰ)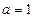 时,求函数
时,求函数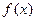 的极值;
的极值;
(Ⅱ)求
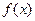 单调区间
单调区间
(Ⅲ)设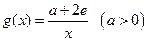 ,若在
,若在 上至少存在一个
上至少存在一个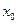 ,使得
,使得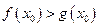 成立,求实数
成立,求实数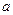 的取值范围。
的取值范围。
已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点。
(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求PC与平面ABCD所成角的正切值;
(Ⅲ)求二面角P一EC一D的正切值。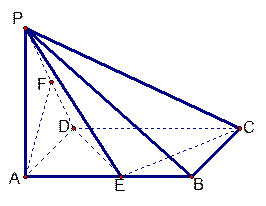
( 12分)奖器有
12分)奖器有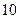 个小球,其中
个小球,其中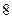 个小球上标有数字
个小球上标有数字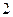 ,
,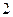 个小球上标有数字
个小球上标有数字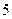 ,现摇出
,现摇出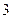 个小球,规定所得奖金(元)为这
个小球,规定所得奖金(元)为这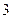 个小球上记号之和,
个小球上记号之和,
(1)求奖金为9元的概率
(2)(非实验班做)求此次摇奖获得奖金数额的分布列
(实 验班做)求此次摇奖获得奖金数额的分布列,期望。.
验班做)求此次摇奖获得奖金数额的分布列,期望。.