选修4﹣2:矩阵与变换
已知二阶矩阵A有特征值λ1=1及对应的一个特征向量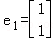 和特征值λ2=2及对应的一个特征向量
和特征值λ2=2及对应的一个特征向量 ,试求矩阵A.
,试求矩阵A.
在△ABC中,角A,B,C的对边分别是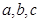 且
且 .
.
(1)求角B的大小;
(2)若 =4,
=4,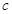 =3,D为BC的中点,求△ABC的面积及AD的长度.
=3,D为BC的中点,求△ABC的面积及AD的长度.
求圆心在直线2x﹣y﹣3=0上,且过点A(5,2)和点B(3,2)的圆的方程.
数列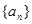 的前
的前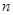 项和为
项和为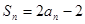 ,
,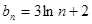 ,函数
,函数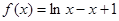 .
.
(1)求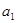 的值和数列
的值和数列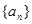 的通项公式;
的通项公式;
(2)证明:当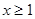 时,
时,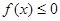 ;
;
(3)求证: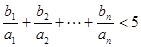 .
.
已知抛物线 与双曲线
与双曲线 有公共焦点
有公共焦点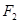 .点
.点 是曲线C1,C2在第一象限的交点,且
是曲线C1,C2在第一象限的交点,且 .
.
(1)求双曲线交点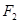 及另一交点
及另一交点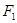 的坐标和点
的坐标和点 的坐标;
的坐标;
(2)求双曲线 的方程;
的方程;
(3)以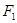 为圆心的圆M与直线
为圆心的圆M与直线 相切,圆N:
相切,圆N: ,过点P(1,
,过点P(1,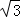 )作互相垂直且分别与圆M、圆N相交的直线
)作互相垂直且分别与圆M、圆N相交的直线 和
和 ,设
,设 被圆M截得的弦长为s,
被圆M截得的弦长为s, 被圆N截得的弦长为t,问:
被圆N截得的弦长为t,问: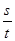 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M是棱BC的中点,DM=2 .
.
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC;
(3)求三棱锥B﹣DOM的体积.