电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.右面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.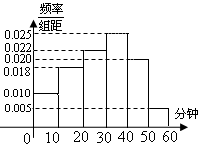
(1)根据已知条件完成下面的 列联表,并据此资料你 是否认为“体育迷”与性别有关?
列联表,并据此资料你 是否认为“体育迷”与性别有关?
| |
非体育迷 |
体育迷 |
合计 |
| 男 |
|
|
|
| 女 |
|
10 |
55 |
| 合计 |
|
|
|
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为 .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求 的分布列,期望
的分布列,期望 和方差
和方差 .
.
附: ,
,
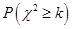 |
0.05 |
0.01 |
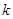 |
3.841 |
6.635 |
已知函数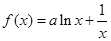
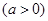 .
.
(Ⅰ)求函数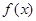 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若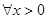 ,均有
,均有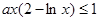 ,求实数
,求实数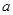 的取值范围.
的取值范围.
(Ⅲ)是否存在实数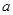 ,使得函数
,使得函数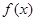 在
在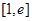 上的最小值为
上的最小值为 ?若存在试求出
?若存在试求出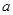 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分13分)已知椭圆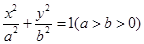 的离心率为
的离心率为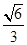 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为 ,直线
,直线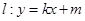 交椭圆于不同的两点
交椭圆于不同的两点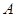 、
、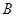 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线 分别切椭圆与圆
分别切椭圆与圆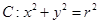 (其中
(其中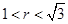 )于
)于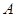 、
、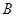 两点,求
两点,求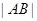 的最大值.
的最大值.
(本小题满分12分)已知数列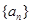 的前
的前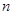 项和
项和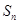 满足:
满足: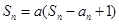 (
(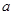 为常数,且
为常数,且 ).且
).且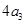 是
是 与
与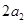 的等差中项,
的等差中项,
(Ⅰ)求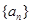 的通项公式;
的通项公式;
(Ⅱ)设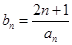 ,数列
,数列 的前
的前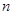 项和为
项和为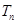 .
.
如图1,在直角梯形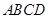 中,
中, ,
,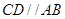 ,
, 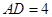 ,
, ,
,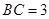 .将
.将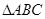 沿
沿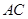 折起,使平面
折起,使平面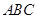
 平面
平面 ,得到几何体
,得到几何体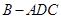 ,如图2所示.
,如图2所示.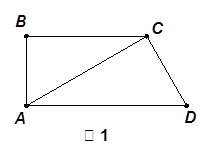
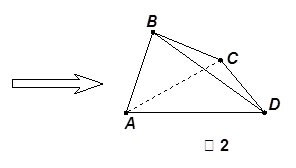
(Ⅰ)求证: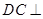 平面
平面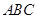 ;
;
(Ⅱ)求二面角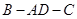 的余弦值.
的余弦值.
2014年中国汽车销售量达到2000多万辆,成为世界汽车销售的冠军,各大品牌与国内自主品牌纷纷加大促销力度,争取2015年实现新的突破.某知名品牌的汽车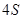 店,对最近
店,对最近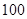 位采用分期付款的购车者进行统计,统计结果如右表所示:已知分
位采用分期付款的购车者进行统计,统计结果如右表所示:已知分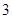 期付款的频率为
期付款的频率为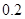 .
.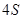 店经销一辆该品牌的汽车,顾客分
店经销一辆该品牌的汽车,顾客分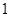 期付款, 其利润为
期付款, 其利润为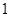 万元;分
万元;分 期或
期或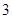 期付款其利润为
期付款其利润为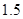 万元;分
万元;分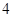 期或
期或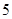 期付款,其利润为
期付款,其利润为 万元.用
万元.用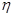 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.
| 付款方式 |
分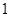 期 期 |
分 期 期 |
分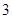 期 期 |
分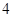 期 期 |
分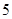 期 期 |
| 频数 |
40 |
20 |
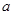 |
10 |
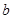 |
(Ⅰ)求上表中的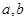 值;
值;
(Ⅱ)若以频率作为概率,求事件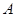 :“购买该品牌汽车的
:“购买该品牌汽车的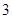 位顾客中,至多有
位顾客中,至多有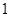 位采用
位采用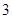 期付款”的概率
期付款”的概率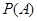 ;
;
(Ⅲ)求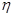 的分布列及数学期望
的分布列及数学期望 .
.