如图在圆锥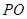 中,已知
中,已知 ,⊙O的直径
,⊙O的直径 ,
, 是弧
是弧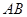 的中点,
的中点,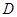 为
为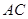 的中点.
的中点.
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
已知圆C: ,是否存在斜率为1的直线
,是否存在斜率为1的直线 ,使以
,使以 被圆C截得的弦AB为直径的圆过原点?若存在,求出直线
被圆C截得的弦AB为直径的圆过原点?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
某市5000名学生参加高中数学毕业会考,得分均在60分以上,现从中随机抽取一个容量为500的样本,制成如图a所示的频率分布直方图.
(1)由频率分布直方图可知本次会考的数学平均分为81分,请估计该市得分在区间 的人数;
的人数;
(2)如图b所示茎叶图是某班男女各4名学生的得分情况,现用简单随机抽样的方法,从这8名学生中,抽取男、女生各一人,求女生得分不低于男生得分的概率.
已知不等式 的解集为
的解集为 .
.
(1)求 ; (2)解关于
; (2)解关于 的不等式
的不等式 .
.
求以 为直径两端点的圆的一般方程.
为直径两端点的圆的一般方程.
((本小题满分12分)
已知点 及圆
及圆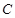 :
: .
.
(1)若直线 过点
过点 且与圆心
且与圆心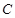 的距离为1,求直线
的距离为1,求直线 的方程;
的方程;
(2)设过点P的直线 与圆
与圆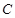 交于
交于 、
、 两点,当
两点,当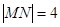 时,求以线段
时,求以线段 为直径的圆
为直径的圆 的方程;
的方程;
(3)设直线 与圆
与圆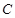 交于
交于 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?若存在,求出实数
?若存在,求出实数 的值;若不存在,请说明理由
的值;若不存在,请说明理由