以原点为极点,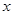 轴的非负半轴为极轴建立极坐标系.已知某圆的极坐标方程为
轴的非负半轴为极轴建立极坐标系.已知某圆的极坐标方程为
(1)将极坐标方程化为普通方程,并选择恰当的参数写出它的参数方程;
(2)若点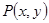 在该圆上,求
在该圆上,求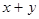 的最大值和最小值.
的最大值和最小值.
设二次函数 的图像过原点,
的图像过原点,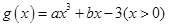 ,
,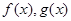 的导函数为
的导函数为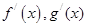 ,且
,且 ,
,

(1)求函数 ,
, 的解析式;
的解析式;
(2)求 的极小值;
的极小值;
(3)是否存在实常数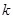 和
和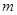 ,使得
,使得 和
和 若存在,求出
若存在,求出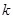 和
和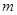 的值;若不存在,说明理由.
的值;若不存在,说明理由.
张林在李明的农场附近建了一个小型工厂,由于工厂生产须占用农场的部分资源,因此李明每年向张林索赔以弥补经济损失并获得一定净收入.工厂在不赔付农场的情况下,工厂的年利润 (元)与年产量
(元)与年产量 (吨)满足函数关系
(吨)满足函数关系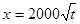 .若工厂每生产一吨产品必须赔付农场
.若工厂每生产一吨产品必须赔付农场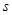 元(以下称
元(以下称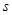 为赔付价格).
为赔付价格).
(Ⅰ)将工厂的年利润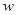 (元)表示为年产量
(元)表示为年产量 (吨)的函数,并求出工厂获得最大利润的年产量;
(吨)的函数,并求出工厂获得最大利润的年产量;
(Ⅱ)若农场每年受工厂生产影响的经济损失金额 (元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格
(元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格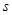 是多少?
是多少?
高三某班有两个数学课外兴趣小组,第一组有 名男生,
名男生, 名女生,第二组有
名女生,第二组有 名男生,
名男生, 名女生.现在班主任老师要从第一组选出
名女生.现在班主任老师要从第一组选出 人,从第二组选出
人,从第二组选出 人,请他们在班会上和全班同学分享学习心得.
人,请他们在班会上和全班同学分享学习心得.
(Ⅰ)求选出的 人均是男生的概率;
人均是男生的概率;
(Ⅱ)求选出的 人中有男生也有女生的概率.
人中有男生也有女生的概率.
如图所示,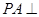 平面
平面 ,四边形
,四边形 为正方形,且
为正方形,且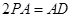 ,
,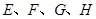 分别是线段
分别是线段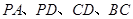 的中点.
的中点.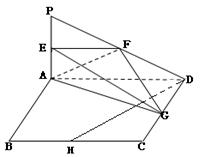
(Ⅰ)求证: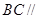 平面
平面 ;
;
(Ⅱ)求证: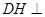 平面
平面 ;
;
(Ⅲ)求三棱锥 与四棱锥
与四棱锥 的体积比.
的体积比.
已知函数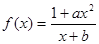
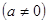 是奇函数,并且函数
是奇函数,并且函数 的图像经过点(1,3),(1)求实数
的图像经过点(1,3),(1)求实数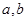 的值;(2)求函数
的值;(2)求函数 的值域.
的值域.