(本小题满分12分)定义在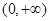 上的函数
上的函数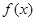 满足下面三个条件:
满足下面三个条件:
①对任意正数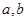 ,都有
,都有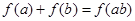 ;
;
②当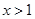 时,
时,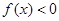 ;
;
③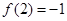 .
.
(1)求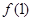 和
和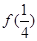 的值;
的值;
(2)试用单调性定义证明:函数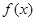 在
在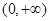 上是减函数;
上是减函数;
(3)求满足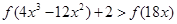 的
的 的取值集合.
的取值集合.
(本小题满分14分)
设锐角三角形ABC的内角A,B,C的对边分别为 ,
,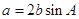
(Ⅰ)求B的大小;
(Ⅱ)求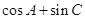 的取值范围
的取值范围
(本小题满分14分)已知向量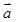 =(
=( ,1),向量
,1),向量 =(sin2x,cos2x),函数
=(sin2x,cos2x),函数
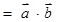
(1)求函数 的表达式,并作出函数
的表达式,并作出函数 在一个周期内的简图(用五点法列表描点);
在一个周期内的简图(用五点法列表描点);
(2)求函数 的周期,并写单调区间.
的周期,并写单调区间.
已知函数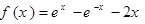 ,
,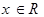
(1)证明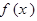 为奇函数,并在
为奇函数,并在 上为增函数;
上为增函数;
(2)若关于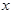 的不等式
的不等式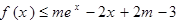 在
在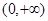 上恒成立,求实数
上恒成立,求实数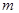 的取值范围
的取值范围
(3)设 ,当
,当 时,
时,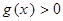 ,求
,求 的最大值
的最大值
设数列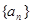 的前
的前 项和为
项和为
(1)若数列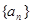 是首项为1,公比为2的等比数列,求常数
是首项为1,公比为2的等比数列,求常数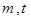 的值,使
的值,使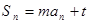 对一切大于零的自然数
对一切大于零的自然数 都成立
都成立
(2)若数列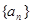 是首项为
是首项为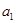 ,公差
,公差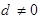 的等差数列,证明:存在常数
的等差数列,证明:存在常数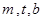 使得
使得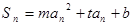 对一切大于零的自然数
对一切大于零的自然数 都成立,且
都成立,且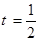
(3)若数列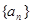 满足
满足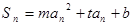 ,
,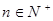 ,
,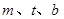 (
(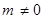 )为常数,且
)为常数,且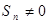 ,证明:当
,证明:当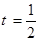 时,数列
时,数列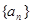 为等差数列
为等差数列
为迎接省运会在我市召开,美化城市,在某主干道上布置系列大型花盆,该圆形花盆直径2米,内部划分为不同区域种植不同花草 如图所示,在蝶形区域内种植百日红,该蝶形区域由四个对称的全等三角形组成,其中一个三角形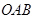 的顶点
的顶点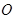 为圆心,
为圆心, 在圆周上,
在圆周上,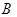 在半径
在半径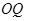 上,设计要求
上,设计要求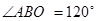

(1)请设置一个变量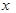 ,写出该蝶形区域的面积
,写出该蝶形区域的面积 关于
关于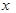 的函数表达式;
的函数表达式;
(2)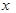 为多少时,该蝶形区域面积
为多少时,该蝶形区域面积 最大?
最大?