某校100位学生期中考试语文成绩的频率分布直方图如图4所示,其中成绩分组区间是: 、
、 、
、 、
、 、
、 .
.
(Ⅰ)求图中 的值;
的值;
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生的语文成绩某些分数段的人数( )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数( )之比如下表所示,求数学成绩在
)之比如下表所示,求数学成绩在 之外的人数.
之外的人数.
| |
||||
| 分数段 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(本小题满分14分)已知数列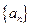 满足对任意的
满足对任意的 ,都有
,都有 ,且
,且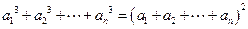 .(1)求
.(1)求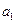 ,
,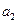 的值;(2)求数列
的值;(2)求数列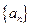 的通项公式
的通项公式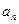 ;(3)设数列
;(3)设数列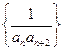 的前
的前 项和为
项和为 ,不等式
,不等式 对任意的正整数
对任意的正整数 恒成立,求实数
恒成立,求实数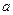 的取值范围.
的取值范围.
(本小题满分14分)已知函数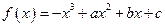 在
在 上是减函数,在
上是减函数,在 上是增函数,函数
上是增函数,函数 在
在 上有三个零点,且1是其中一个零点.(1)求
上有三个零点,且1是其中一个零点.(1)求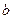 的值;(2)求
的值;(2)求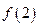 的取值范围;(3)试探究直线
的取值范围;(3)试探究直线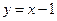 与函数
与函数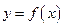 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.
(本小题满分14分)已知动点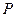 到定点
到定点 的距离与点
的距离与点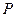 到定直线
到定直线 :
: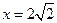 的距离之比为
的距离之比为 .(1)求动点
.(1)求动点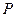 的轨迹
的轨迹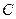 的方程;(2)设
的方程;(2)设 、
、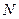 是直线
是直线 上的两个点,点
上的两个点,点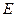 与点
与点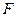 关于原点
关于原点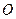 对称,若
对称,若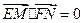 ,求
,求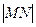 的最小值.
的最小值.
(本小题满分12分)已知直线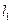 :
: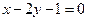 ,直线
,直线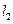 :
: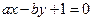 ,其中
,其中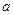 ,
,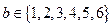 .(1)求直线
.(1)求直线 的概率;(2)求直线
的概率;(2)求直线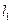 与
与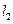 的交点位于第一象限的概率.
的交点位于第一象限的概率.
(本小题满分14分)
如图6,正方形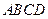 所在平面与三角形
所在平面与三角形 所在平面相交于
所在平面相交于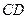 ,
, 平面
平面 ,且
,且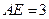 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求凸多面体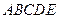 的体积.
的体积.