已知双曲线 ,过
,过 能否作一条直线
能否作一条直线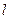 ,与双曲线交于
,与双曲线交于 两点,且点
两点,且点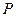 是线段
是线段 中点?若能,求出
中点?若能,求出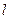 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
(本小题满分14分)如图所示,椭圆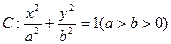 的离心率为
的离心率为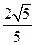 ,且A(0,1)是椭圆C的顶点。
,且A(0,1)是椭圆C的顶点。
(1)求椭圆C的方程;
(2)过点A作斜率为1的直线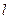 ,设以椭圆C的右焦点F为抛物线
,设以椭圆C的右焦点F为抛物线 的焦点,若点M为抛物线E上任意一点,求点M到直线
的焦点,若点M为抛物线E上任意一点,求点M到直线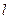 距离的最小值。
距离的最小值。
某工厂生产一种产品的成本费由三部分组成:① 职工工资固定支出 元;② 原材料费每件40元;③ 电力与机器保养等费用为每件
元;② 原材料费每件40元;③ 电力与机器保养等费用为每件 元,其中
元,其中 是该厂生产这种产品的总件数.
是该厂生产这种产品的总件数.
(1)把每件产品的成本费P(x)(元)表示成产品件数 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量 不超过
不超过 件,且产品能全部销售.根据市场调查:每件产品的销售价
件,且产品能全部销售.根据市场调查:每件产品的销售价 与产品件数
与产品件数 有如下关系:
有如下关系: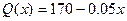 ,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
(本小题满分14分)
已知数列 是首项为1,公比为2的等比数列,数列
是首项为1,公比为2的等比数列,数列 的前
的前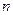 项和
项和 .
.
(1)求数列 与
与 的通项公式;
的通项公式;
(2)求数列 的前
的前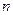 项和.
项和.
(本小题共14分)
已知直三棱柱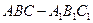 的所有棱长都相等,且
的所有棱长都相等,且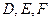
分别为 的中点.
的中点.
(Ⅰ) 求证:平面 平面
平面 ;
;
(Ⅱ)求证: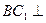 平面
平面 .
.