某工厂生产一种产品的成本费由三部分组成:① 职工工资固定支出 元;② 原材料费每件40元;③ 电力与机器保养等费用为每件
元;② 原材料费每件40元;③ 电力与机器保养等费用为每件 元,其中
元,其中 是该厂生产这种产品的总件数.
是该厂生产这种产品的总件数.
(1)把每件产品的成本费P(x)(元)表示成产品件数 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量 不超过
不超过 件,且产品能全部销售.根据市场调查:每件产品的销售价
件,且产品能全部销售.根据市场调查:每件产品的销售价 与产品件数
与产品件数 有如下关系:
有如下关系: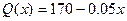 ,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
给出 下面的数表序列:
下面的数表序列:
其中表n(n="1,2,3"  )有n行,第1行的n个数是1,3,5,
)有n行,第1行的n个数是1,3,5, 2n-1,从第2行起
2n-1,从第2行起 ,每行中的每个数都等
,每行中的每个数都等 于它肩上的两数之和。
于它肩上的两数之和。
(I)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明);
(II)每个数列中最后一行都只有一个数,它们构成数列1,4,12
 ,记此数列为
,记此数列为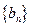 求和:
求和: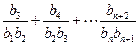
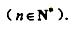
设各项均为正数的数列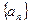 的前n项和为
的前n项和为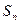 ,已知
,已知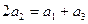 ,数
,数
列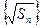 是公差为
是公差为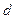 的等差数列。
的等差数列。
(1)求数列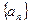 的通项公式(用
的通项公式(用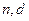 表示);
表示);
(2)设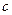 为实数,对满足
为实数,对满足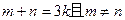 的任意正整数
的任意正整数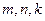 ,不等式
,不等式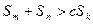 都成立。求证:
都成立。求证: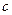 的最大值为
的最大值为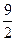 。
。
设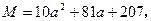
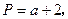
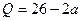 ,若将
,若将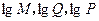
适当排序后可构成公差为1的等差数列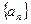 的前三项.
的前三项.
(Ⅰ)求
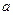 的值及
的值及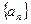 的通项公式;
的通项公式;
(Ⅱ )记函数
)记函数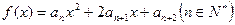 的图象在
的图象在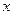 轴上截得的线段长为
轴上截得的线段长为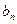 ,设
,设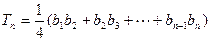 ,求
,求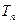
 证明以下命题:
证明以下命题:
(Ⅰ)对任一正整a,都存在整数b,c(b<c),使得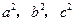 成等差数列。
成等差数列。
(Ⅱ)存在无穷多个互不相似的三角形△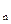 ,其边长
,其边长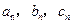 为正整数且
为正整数且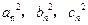 成等差数列。
成等差数列。
在数列 中,
中, =0,且对任意k
=0,且对任意k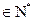 ,
, 成等差数列,
成等差数列,
其公差为2k。
(Ⅰ)证明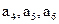 成等比数列;
成等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;