(本小题满分13分)
已知函数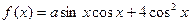 ,
, ,
,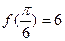 .
.
(Ⅰ)求常数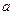 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数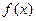 的最小正周期和最大值.
的最小正周期和最大值.
设椭圆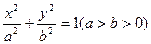 的焦点分别为
的焦点分别为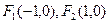 ,直线
,直线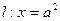 交
交 轴于点
轴于点 ,且
,且 .
.
(1)试求椭圆的方程;
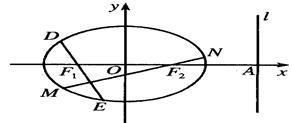
(2)过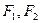 分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形
分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形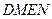 面积的最大值和最小值.
面积的最大值和最小值.
已知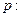 方程
方程 有两个不等的负根;
有两个不等的负根; 方程
方程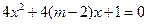 无实根,若
无实根,若 或
或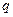 为真,
为真, 且
且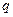 为假,求
为假,求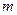 的取值范围。
的取值范围。
已知抛物线C: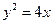 ,
,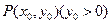 为抛物线上一点
为抛物线上一点 ,
, 为
为 关于
关于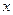 轴对称的点,
轴对称的点,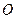 为坐标原点.
为坐标原点.
(1)若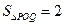 ,求
,求 点的坐标;
点的坐标;
(2)若过满足 (1)中的点
(1)中的点 作直线
作直线 交抛物线
交抛物线 于
于 两点, 且斜率分别为
两点, 且斜率分别为 ,且
,且 ,求证:直线
,求证:直线 过定点,并求出该定点坐标
过定点,并求出该定点坐标
已知双曲线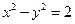
(1)求以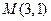 为中点的弦所在的直线的方程
为中点的弦所在的直线的方程
(2)求过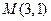
 的弦的中点的轨迹方程
的弦的中点的轨迹方程