设椭圆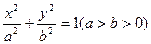 的焦点分别为
的焦点分别为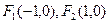 ,直线
,直线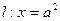 交
交 轴于点
轴于点 ,且
,且 .
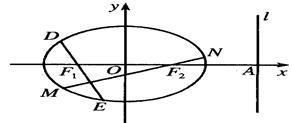
.
(1)试求椭圆的方程;
(2)过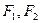 分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形
分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形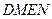 面积的最大值和最小值.
面积的最大值和最小值.
某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点. 
(1)根据三视图,画出该几何体的直观图;
(2)在直观图中,①证明PD∥面AGC;②证明面PBD⊥面AGC.
底面是平行四边形的四棱锥P-ABCD,点E在PD上,且PE∶ED=2∶1.
问:在棱PC上是否存在一点F,使BF∥面AEC?证明你的结论.
如图(1),△BCD内接于直角梯形A1A2A3D,已知沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图(2)所示. 
(1)求证:在三棱锥ABCD中,AB⊥CD;
(2)若直角梯形的上底A1D=10,高A1A2=8,求翻折后三棱锥的侧面ACD与底面BCD所成二面角θ的余弦值.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.求证:PA∥平面EDB. 
如图,已知斜三棱柱ABC-A1B1C1的底面△ABC为直角三角形,∠C=90°,侧棱与底面成60°角,点B1在底面的射影D为BC的中点. 
求证:AC⊥平面BCC1B1.