如图所示，在平面直角坐标系第Ⅲ象限内充满＋y 方向的匀强电场， 在第Ⅰ象限的某个圆形区域内有垂直于纸面的匀强磁场（电场、磁场均未画出）；一个比荷为
的带电粒子以大小为 v 0的初速度自点
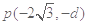沿＋x 方向运动，恰经原点O进入第Ⅰ象限，粒子穿过匀强磁场后，最终从 x轴上的点 Q（9d,0 ）沿－y 方向进入第Ⅳ象限；已知该匀强磁场的磁感应强度为 
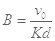，不计粒子重力。 
（1）求第Ⅲ象限内匀强电场的场强E的大小；
（2）求粒子在匀强磁场中运动的半径R及时间t B；
（3）求圆形磁场区的最小半径rm。
如图所示，质量均为m的小车与木箱紧挨着静止在光滑的水平冰面上，质量为2m的小明站在小车上用力向右迅速推出木箱，木箱相对于冰面的速度为v，接着木箱与右侧竖直墙壁发生弹性碰撞，反弹后被小明接住，求：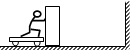
（i）推出木箱后小明和车的速度大小和方向；
（ii）小明接住木箱后三者共同速度的大小。
某同学做“测定玻璃折射率”实验时，完成光路图后，由于没有量角器，借助圆规以O为圆心画圆，分别交入射光线于A点，交OO′连线延长线于C点。分别过A点、C点作法线NN′的垂线AB、CD交NN′于B点、D点，用刻度尺量得AB=l0cm，CD =6cm，求：
（i）玻璃的折射率n；
（ii）光从这种玻璃进入空气时的临界角。
一定质量的理想气体体积V与热力学温度T的关系图象如图所示，气体在状态A时的压强pA=p0，温度TA=T0，线段AB与V轴平行，BC的延长线过原点。求：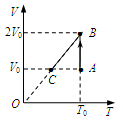
（i）气体在状态B时的压强pB；
（ii）气体从状态A变化到状态B的过程中，对外界做的功为10J，该过程中气体吸收的热量为多少；
（iii）气体在状态C时的压强pC和温度TC。
有人设想用如图所示的装置来选择密度相同、大小不同的球状纳米颗粒．颗粒在电离室中电离后带正电，电量与其表面积成正比．电离后，颗粒缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I（加速距离极短，忽略此过程中重力的影响），再通过小孔O2射入匀强电场区域II，区域II中极板长度为l，极板间距为d．收集室的小孔O3与O1、O2在同一条水平线上且到上下极板的距离相等．半径为r0的颗粒，其质量为m0、电量为q0，刚好能沿O1O3直线射入收集室．（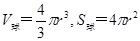
）试求：
（1）图中区域II的电场强度；
（2）半径为r的颗粒通过O2时的速率；
（3）落到区域II中的下极板上的颗粒半径．
某兴趣小组设计了如图所示的玩具轨道，它由细圆管弯成，固定在竖直平面内．左右两侧的斜直管道PA与PB的倾角、高度、粗糙程度完全相同，管口A、B两处均用很小的光滑小圆弧管连接（管口处切线竖直），管口到底端的高度H1="0.4" m．中间“8”字型光滑细管道的圆半径R="10" cm（圆半径比细管的内径大得多），并与两斜直管道的底端平滑连接．一质量m="0.5" kg的小滑块从管口 A的正上方H2="5" m处自由下落，滑块第一次到达“8”字型管道顶端时对轨道外侧Q点的压力大小为F="455" N．此后小滑块经“8”字型和PB管道运动到B处竖直向上飞出，然后又再次落回，如此反复．小滑块视为质点，忽略小滑块进入管口时因碰撞造成的能量损失，不计空气阻力，且取g="10" m/s2．求：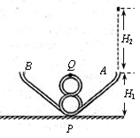
（1）滑块第一次由A滑到P的过程中，克服摩擦力做功；
（2）滑块第一次离开管口B后上升的高度；
（3）滑块能冲出槽口的次数．