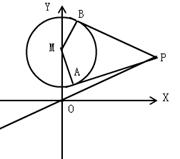
(本小题满分12分)如图, 已知圆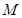 :
: 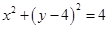 , 直线
, 直线 的方程为
的方程为 , 点
, 点 是直线
是直线 上一动点, 过点
上一动点, 过点 作圆的切线
作圆的切线 、
、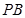 , 切点为
, 切点为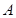 、
、 .
.
(1)当 的横坐标为
的横坐标为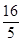 时, 求∠
时, 求∠ 的大小;
的大小;
(2)求证: 经过A、P、M三点的圆 必过定点, 并求出所有定点的坐标.
必过定点, 并求出所有定点的坐标.
(本小题满分12分)如图所示,矩形 中,
中, ,
,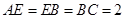 ,
, ,且
,且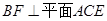 ,
, 交于点
交于点 。
。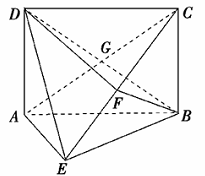
(1)求证: ;
;
(2)求三棱锥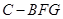 的体积.
的体积.
(本小题满分12分)某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
| 喜欢 |
不喜欢 |
合计 |
|
| 大于40岁 |
20 |
5 |
25 |
| 20岁至40岁 |
10 |
20 |
30 |
| 合计 |
30 |
25 |
55 |
(1)判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关?
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
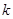 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: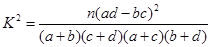 ,其中
,其中 )
)
(本小题满分12分)如图,在 中,已知
中,已知 ,
, 是
是 边上的一点,
边上的一点,

(1)求 的值;
的值;
(2)求 的值.
的值.
(本小题满分10分)已知等比数列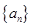 前
前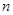 项和为
项和为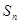 ,且满足
,且满足 ,
,
(1)求数列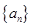 的通项公式;
的通项公式;
(2)求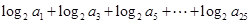 的值
的值
(本小题满分12分) 设函数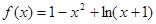
(1)求函数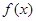 的单调区间;
的单调区间;
(2)若不等式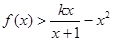 (
(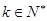 )在
)在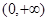 上恒成立,求
上恒成立,求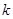 的最大值.
的最大值.