设等差数列
的公差为
,前
项和为
,等比数列
的公比为
.已知
.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)当
时,记
,求数列
的前
项和
.
某同学用"五点法"画函数
在某一个周期内的图象时,列表并填入了部分数据,如下表:
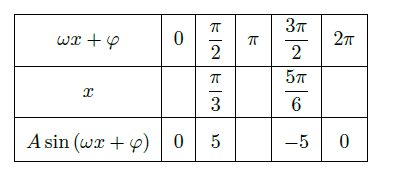
(Ⅰ)请将上表数据补充完整,并直接写出函数
的解析式;
(Ⅱ)将
图象上所有点向左平行移动
个单位长度,得到
的图象.若
图象的一个对称中心为
,求
的最小值.
设
为实数,函数
.
(1)若
,求
的取值范围;
(2)讨论
的单调性;
(3)当
时,讨论
在区间
内的零点个数.
已知过原点的动直线
与圆
相交于不同的两点
.
(1)求圆
的圆心坐标;
(2)求线段
的中点
的轨迹
的方程;
(3)是否存在实数
,使得直线
与曲线
只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
设数列
的前
项和为
,
.已知
,且当
时,
.
(1)求
的值;
(2)证明:
为等比数列;
(3)求数列
的通项公式.