(本小题满分15分)如图,已知抛物线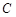 :
: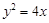 ,过焦点
,过焦点 斜率大于零的直线
斜率大于零的直线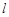 交抛物线于
交抛物线于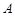 、
、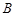 两点,且与其准线交于点
两点,且与其准线交于点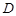 .
.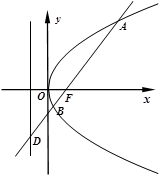
(Ⅰ)若线段 的长为
的长为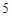 ,求直线
,求直线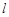 的方程;
的方程;
(Ⅱ)在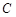 上是否存在点
上是否存在点 ,使得对任意直线
,使得对任意直线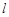 ,直线
,直线 ,
,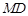 ,
,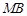 的斜率始终成等差数列,若存在求点
的斜率始终成等差数列,若存在求点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知集合 ,集合
,集合
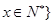 ,集合
,集合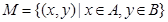
(1)求从集合 中任取一个元素是(3,5)的概率;
中任取一个元素是(3,5)的概率;
(2)从集合 中任取一个元素,求
中任取一个元素,求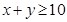 的概率;
的概率;
(3)设 为随机变量,
为随机变量,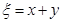 ,写出
,写出 的分布列,并求
的分布列,并求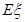 。
。
在 中,
中,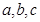 分别是角
分别是角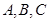 的对边,若
的对边,若 ,
, 。
。
(1)求角 的大小;
的大小;
(2)若 求
求 面积
面积
如图,直角梯形ABMN中,∠NAB=90°,AN∥BM,AB=2,AN= ,BM=
,BM= ,椭圆C以A,B为焦点且过点N.
,椭圆C以A,B为焦点且过点N.
(1)建立适当的坐标系,求椭圆C方程;
(2)若点E满足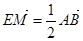 ,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由?
,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由?
如图,ABCD是边长为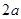 的正方形,ABEF是矩形,且二面角C
的正方形,ABEF是矩形,且二面角C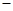 AB
AB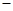 F是直二面角,
F是直二面角,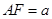 ,G是EF的中点,
,G是EF的中点,
(1)求GB与平面AGC所成角的正弦值.
(2)求二面角B—AC—G的余弦值.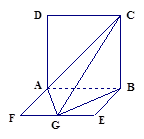
已知 ,讨论方程
,讨论方程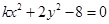 所表示的圆锥曲线类型,并求其焦点坐标
所表示的圆锥曲线类型,并求其焦点坐标