(本小题满分12分)已知函数 .
.
(1)若曲线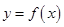 在
在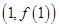 处的切线为
处的切线为 ,求
,求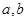 的值;
的值;
(2)若函数 在
在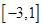 上是单调函数,求实数
上是单调函数,求实数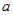 的取值范围;
的取值范围;
(3)若 有两个不同极值点
有两个不同极值点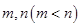 ,且
,且 ,记
,记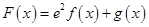 ,求
,求 的最大值.
的最大值.
如图,在四面体ABCD中,CB="CD," AD⊥BD,点E、F分别是AB, BD的中点,求证:
(1)直线EF//平面ACD;
(2)平面EFC⊥平面BCD。
(本题18分)
已知:正数数列 的通项公式
的通项公式

(1)求数列 的最大项;
的最大项;
(2)设 ,确定实常数
,确定实常数 ,使得
,使得 为等比数列;
为等比数列;
(3)(理)数列 ,满足
,满足 ,
, ,其中
,其中 为第(2)小题中确定的正常数,求证:对任意
为第(2)小题中确定的正常数,求证:对任意 ,有
,有 且
且 或
或 且
且 成立.
成立.
(文)设 是满足第(2)小题的等比数列,求使不等式
是满足第(2)小题的等比数列,求使不等式 成立的最小正整数
成立的最小正整数 .
.
(本题16分)
如图,F是抛物线 的焦点,Q是准线与
的焦点,Q是准线与 轴的交点,斜率为
轴的交点,斜率为 的直线
的直线 经过点Q.
经过点Q.
(1)当K取不同数值时,求直线 与抛物线交点的个数;
与抛物线交点的个数;
(2)如直线 与抛物线相交于A、B两点,求证:
与抛物线相交于A、B两点,求证: 是定值
是定值
(3)在 轴上是否存在这样的定点M,对任意的过点Q的直线
轴上是否存在这样的定点M,对任意的过点Q的直线 ,如
,如 与抛物线相交于A、B两点,均能使得
与抛物线相交于A、B两点,均能使得 为定值,有则找出满足条
为定值,有则找出满足条
件的点M;没有,则说明理由.
(本题16分)
如图所示,某人在斜坡P处仰视正对 面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为
面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为 ,
,
(1)以射线OC为 轴的正向,OB为
轴的正向,OB为 轴正向,建立直角坐标系,求
轴正向,建立直角坐标系,求 出斜坡CD所在直线方程;
出斜坡CD所在直线方程;
(2)当观察者P视角∠APB最大时,求点P的坐标(人的身高忽略不计).
(本题14分)
△ABC中,角A、B、C的对边依次为 、
、 、
、 .已知
.已知 ,
, ,外接圆半径
,外接圆半径 ,
, 边长为整数,
边长为整数,
(1)求∠A的大小(用反三角函数表示);
(2)求边长 ;
;
(3)在AB、AC上分别有点D、E,线段DE将△ABC分成面积相等的两部分,求线段DE长的最小值.