(本小题满分12分)甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲、乙、丙面试合格的概率分别是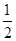 ,
,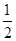 ,
,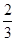 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(Ⅰ)至少有1人面试合格的概率;
(Ⅱ)签约人数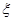 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
已知f(x)=
 ,求f[f(0)]的值
,求f[f(0)]的值
(本小题满分12分)
集合A={(x,y) },集合B={(x,y)
},集合B={(x,y) ,且0
,且0 },又A
},又A ,求实数m的取值范围
,求实数m的取值范围
(本小题满分12分)
已知,全集U={x|-5≤x≤3},A={x|-5≤x<-1},B={x|-1≤x<1},求CUA,CUB,(CUA)∩(CUB),(CUA)∪(CUB),CU(A∩B),CU(A∪B),并指出其中相关的集合
(本 小题满分14分)
小题满分14分) 已知
已知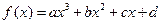 是定义在
是定义在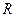 上的函数, 其
上的函数, 其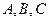 三点, 若点
三点, 若点 的坐标为
的坐标为
 ,且
,且  在
在 和
和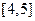 上有相同的单调性, 在
上有相同的单调性, 在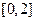 和
和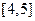 上有相反的单调性.
上有相反的单调性.
(1)求 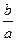 的取值范围;
的取值范围;
(2)在函数 的图象上是否存在一点
的图象上是否存在一点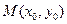 , 使得
, 使得  在点
在点 的切线斜率为
的切线斜率为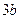 ?求出点
?求出点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)求 的取值范围。
的取值范围。
.本小题满分15分)
如图,已知椭圆E:
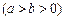 ,焦点为
,焦点为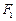 、
、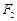 ,双曲线G:
,双曲线G: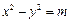
 的顶点是该椭
的顶点是该椭 圆的焦点,设
圆的焦点,设 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线 、
、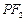 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形 的周长等于
的周长等于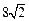 ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为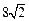 .
.
(1)求椭圆E与双曲线G的方程;
(2)设直线 、
、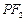 的斜率分别为
的斜率分别为 和
和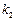 ,探求
,探求 和
和
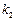 的关系;
的关系;
(3)是否存在常数 ,使得
,使得 恒成立?
恒成立?
若存在,试求出 的值;若不存在, 请说明理由.
的值;若不存在, 请说明理由.