已知数列 与
与 ,若
,若 且对任意正整数
且对任意正整数 满足
满足 数列
数列 的前
的前 项和
项和 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列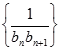 的前
的前 项和
项和
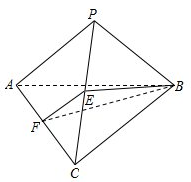
如图,在三棱锥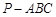 中,点
中,点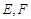 分别是棱
分别是棱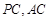 的中点.
的中点.
(1)求证: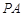 //平面
//平面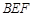 ;
;
(2)若平面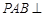 平面
平面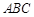 ,
,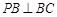 ,求证:
,求证: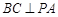 .
.
在△ABC中,角A,B,C的对边分别为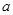 ,
,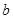 ,
,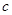 ,且
,且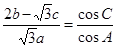 .
.
(1)求角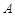 的值;
的值;
(2)若角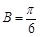 ,
,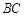 边上的中线
边上的中线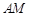 =
=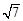 ,求
,求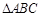 的面积.
的面积.
设数列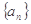 的前
的前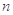 项和为
项和为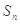 ,对一切
,对一切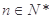 ,点
,点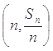 都在函数
都在函数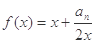 的图象上
的图象上
(1)求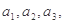 归纳数列
归纳数列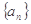 的通项公式(不必证明);
的通项公式(不必证明);
(2)将数列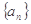 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为(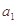 ),
),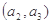 ,
,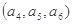 ,
,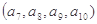 ;
;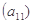 ,
,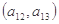 ,
, ,
,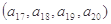 ;
;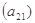 ,…..,
,…..,
分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为 ,
,
求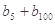 的值;
的值;
(3)设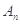 为数列
为数列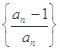 的前
的前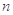 项积,若不等式
项积,若不等式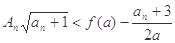 对一切
对一切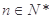 都成立,其中
都成立,其中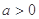 ,求
,求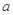 的取值范围
的取值范围
设数列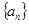 为等差数列,且
为等差数列,且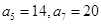 ,数列
,数列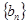 的前
的前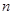 项和为
项和为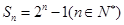 ,
,
(1)求数列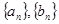 的通项公式;
的通项公式;
(2)若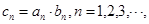 ,求数列
,求数列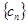 的前
的前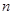 项和
项和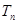 .
.
已知 三个内角
三个内角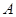 ,
, ,
,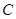 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,
,
(1)求角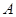
(2)若 =
= ,
, 的面积为
的面积为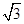 ,求
,求 的周长.
的周长.