甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计)即为中奖.
乙商场:从装有3个白球3个红球的盒子中一次性摸出2球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.
问:购买该商品的顾客在哪家商场中奖的可能性大?
已知集合A=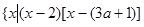
 ,集合B=
,集合B=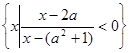 。
。
当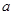 =2时,求
=2时,求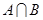 ;
;
当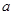
 时,若元素
时,若元素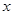
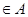 是
是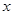
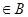 的必要条件,求实数
的必要条件,求实数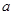 的取值范围。
的取值范围。
(本小题满分12分)四棱锥 中,底面
中,底面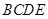 为矩形,侧面
为矩形,侧面 底面
底面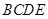 ,
,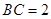 ,
,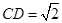 ,
,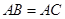 .
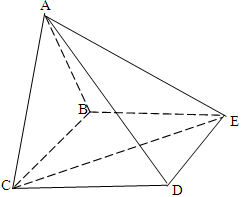
.
(Ⅰ)证明: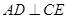 ;
;
(Ⅱ)设 与平面
与平面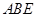 所成的角为
所成的角为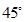 ,
,
求二面角 的余弦值.
的余弦值.
(本小题满分12分)已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且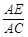 =
=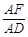 =λ (0<λ<1).
=λ (0<λ<1).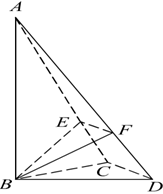
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时?平面BEF⊥平面ACD.
(本小题满分12分)如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离.
(本小题满分12分)如图,在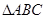 中,
中, 是
是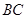 上的高,沿
上的高,沿 把
把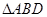 折起,使
折起,使 。
。
(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设E为BC的中点,求AE与DB夹角的余弦值。