如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为1cm,矩形ABCD的边AD、AB分别与l1,l2重合,AB=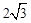 cm,AD=2cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为2cm/s,矩形ABCD的移动速度为3cm/s,设移动时间为t(s).
cm,AD=2cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为2cm/s,矩形ABCD的移动速度为3cm/s,设移动时间为t(s).
(1)如图①,连接OA、AC,则∠OAC的度数为 °;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<1时,求t的取值范围(解答时可以利用备用图画出相关示意图).
如图,直线AB是某天然气公司的主输气管道,点C、D是在AB异侧的两个小区,现在主输气管道上寻找支管道连接点,铺设管道向两个小区输气.有以下两个方案:
方案一:只取一个连接点P,使得向两个小区铺设的支管道总长度最短;
方案二:取两个连接点M和N,使得点M到C小区铺设的支管道最短,使得点N到D小区铺设的管道最短.om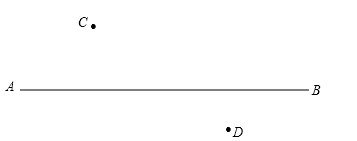
(1)在图中标出点P、M、N的位置,保留画图痕迹;
(2)设方案一中铺设的支管道总长度为L1,方案二中铺设的支管道总长度为L2,则L1与L2的大小关系为:L1L2(填“>”、“<”或“=”).
在y=ax2+bx+c中,当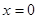 时,y=
时,y=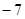 ;
;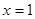 时,y=
时,y=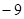 ;
; 时,y=
时,y= ,求
,求 的值.
的值.
如图,AB∥CD,BE平分∠ABC,∠DCB=140°,求∠ABD和∠EDC的度数.
已知 求
求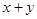 的算术平方根.
的算术平方根.
(1)解方程: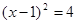
(2)解方程组: