(本小题满分12分)甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下: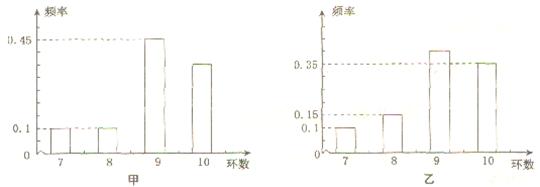
若将频率视为概率,回答下列问题.(Ⅰ)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率; (Ⅱ)若甲、乙两运动员各自射击1次,ξ表示这2次射击中击中9环以上(含9环)的次数,求ξ的分布列及Eξ.
((本小题满分12分)
已知数列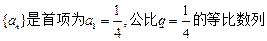 ,设
,设 ,数列
,数列 .(Ⅰ)求数列
.(Ⅰ)求数列 的通项公式;(Ⅱ)若数列
的通项公式;(Ⅱ)若数列 的前
的前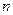 项和为
项和为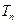 ,求
,求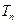 .
.
已知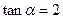 ,则
,则 的值等于
的值等于
(本小题满分14分)若椭圆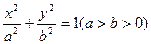 过点
过点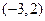 ,离心率为
,离心率为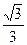 ,⊙O的圆心在原点,直径为椭圆的短轴,⊙M的方程为
,⊙O的圆心在原点,直径为椭圆的短轴,⊙M的方程为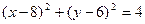 ,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B. (1) 求椭圆的方程;(2)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的方程。
,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B. (1) 求椭圆的方程;(2)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的方程。
(本小题满分14分) 如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
(1)求证:EF∥平面CB1D1;(2)求证:平面CAA1C1⊥平面CB1D1.