在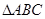 中,角
中,角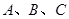 所对的边分别为
所对的边分别为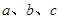 ,若
,若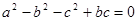 。
。
(1)求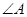 的大小;
的大小;
(2)设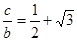 ,求
,求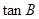 的值。
的值。
(满分12分)
已知命题P:函数
命题q:方程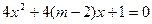 无实根。
无实根。
若p或q为真,p且q为假,求实数m的取值范围
(本小题满分13分)
设函数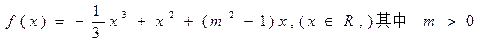
(1)当 曲线
曲线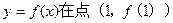 处的切线斜率
处的切线斜率
(2)求函数的单调区间与极值;
(3)已知函数 有三个互不相同的零点0,
有三个互不相同的零点0, ,且
,且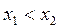 。若对任意的
。若对任意的 ,
, 恒成立,求m的取值范围。
恒成立,求m的取值范围。
设 分别是椭圆C:
分别是椭圆C: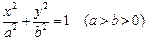 的左右焦点,
的左右焦点,
(1)设椭圆C上的点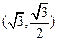 到
到 两点距离之和等于4,写出椭圆C的方程和焦点坐标。
两点距离之和等于4,写出椭圆C的方程和焦点坐标。
(2)设K是(1)中所得椭圆上的动点,求线段 的中点B的轨迹方程。
的中点B的轨迹方程。
(3 )设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为
)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为 试探究
试探究 的值是否与点P及直线L有关,并证明你的结论。
的值是否与点P及直线L有关,并证明你的结论。
(本题满分13分)
机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值);
(3)使用若干年后,对机床的处理方案有两种:
(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
(本题满分12分)
投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.现知某人在以前投掷1000次的试验中,有500次入红袋,250次入蓝袋,其余不能入袋
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2) 求该人两次投掷后得分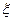 的分布列和数学期望.
的分布列和数学期望.