(本小题满分12分)已知椭圆E的方程: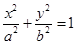 (
( ),它的两个焦点为
),它的两个焦点为 ,P为椭圆的一点(点
,P为椭圆的一点(点 在第三象限上), 且
在第三象限上), 且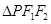 的周长为
的周长为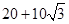 ,
,
(Ⅰ)求椭圆E的方程;
(Ⅱ)若以点P为圆心的圆过椭圆的左顶点M与点 , MP交圆P与另一点N,若点A在椭圆E上,使得
, MP交圆P与另一点N,若点A在椭圆E上,使得 ,求点A的坐标.
,求点A的坐标.
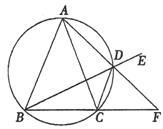
已知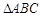 中,
中,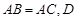 为
为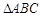 外接圆劣弧
外接圆劣弧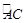 上的点(不与点
上的点(不与点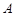 .
.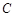 重合),延长
重合),延长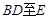 ,延长
,延长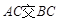 的延长线于
的延长线于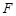 .
.
(1)求证: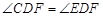 ;
;
(2)求证: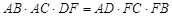 .
.
已知函数 .
.
(1)当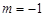 时,求函数
时,求函数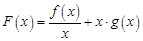 在
在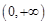 上的极值;
上的极值;
(2)若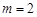 ,求证:当
,求证:当 时,
时,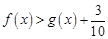 .
.
(参考数据: )
)
已知椭圆 的离心率为
的离心率为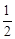 ,左.右焦点分别是
,左.右焦点分别是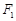 ,
, ,点
,点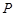 为椭圆
为椭圆 上任意一点,且
上任意一点,且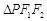 面积最大值为
面积最大值为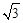 .
.
(1)求椭圆 的方程;
的方程;
(2)过 作垂直于
作垂直于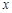 轴的直线
轴的直线 交椭圆于
交椭圆于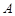 .
. 两点(点
两点(点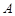 在第一象限),
在第一象限), .
. 是椭圆上位于直线
是椭圆上位于直线 两侧的动点,若
两侧的动点,若 ,求证:直线
,求证:直线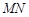 的斜率为定值.
的斜率为定值.
已知抛物线 的焦点为
的焦点为 ,抛物线
,抛物线 的焦点为
的焦点为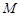 .
.
(1)若过点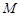 的直线
的直线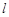 与抛物线
与抛物线 有且只有一个交点,求直线
有且只有一个交点,求直线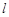 的方程;
的方程;
(2)若直线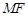 与抛物线
与抛物线 交于
交于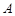 .
. 两点,求
两点,求 的面积.
的面积.
在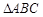 中,已知角
中,已知角 .
.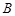 .
.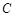 的对边分别为
的对边分别为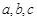 ,且
,且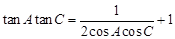 .
.
(1)求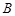 的大小;
的大小;
(2)若 ,试判断
,试判断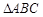 的形状.
的形状.