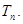过函数 的图象上任意一点
的图象上任意一点 的切线与
的切线与 轴交于点
轴交于点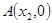 ,求证:
,求证: .
.
已知函数
(1)当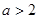 时,求函数
时,求函数 极小值;
极小值;
(2)试讨论曲线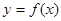 与
与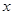 轴公共点的个数。
轴公共点的个数。
如图,四边形ABCD是一块边长为4的正方形地域,地域内有一条河流MD,其经过的路线是以AB中点M为顶点,且开口向右的抛物线(河流宽度不计)。某公司准备建一大型游乐园PQCN,问如何施工,才能使游乐园面积最大?并求出最大的面积。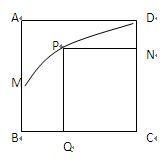
在直角坐标平面上有一点列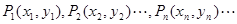 ,对一切正整数
,对一切正整数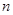 ,点
,点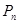 位于函数
位于函数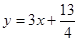 的图象上,且
的图象上,且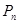 的横坐标构成以
的横坐标构成以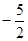 为首项,
为首项, 为公差的等差数列
为公差的等差数列 。
。
⑴求点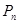 的坐标;
的坐标;
⑵设抛物线列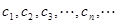 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于 轴,第
轴,第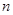 条抛物线
条抛物线 的顶点为
的顶点为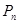 ,且过点
,且过点 ,记与抛物线
,记与抛物线 相切于
相切于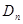 的直线的斜率为
的直线的斜率为 ,求:
,求: 。
。
⑶设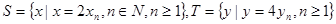 ,等差数列
,等差数列 的任一项
的任一项 ,其中
,其中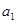 是
是 中的最大数,
中的最大数, ,求
,求 的通项公式。
的通项公式。
已知数列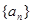 ,设Sn是数列的前n项和,并且满足a1=1,对任意正整数n,
,设Sn是数列的前n项和,并且满足a1=1,对任意正整数n,
(1)令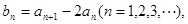 证明
证明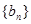 是等比数列,并求
是等比数列,并求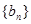 的通项公式;
的通项公式;
(2)令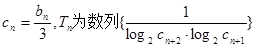 的前n项和,求
的前n项和,求