(本小题满分10分)选修4-5:不等式选讲
已知函数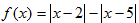
(1)若关于 的不等式
的不等式 有解,求
有解,求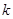 的最大值;
的最大值;
(2)求不等式: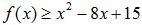 的解集.
的解集.
已知双曲线经过点M( ),且以直线x= 1为右准线.
),且以直线x= 1为右准线.
(1)如果F(3,0)为此双曲线的右焦点,求双曲线方程;
(2)如果离心率e=2,求双曲线方程.
已知椭圆: 上的两点A(0,
上的两点A(0, )和点B,若以AB为边作正△ABC,当B变动时,计算△ABC的最大面积及其条件.
)和点B,若以AB为边作正△ABC,当B变动时,计算△ABC的最大面积及其条件.
已知抛物线C的准线为x =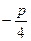 (p>0),顶点在原点,抛物线C与直线l:y =x-1相交所得弦的长为3
(p>0),顶点在原点,抛物线C与直线l:y =x-1相交所得弦的长为3 ,求
,求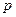 的值和抛物线方程.
的值和抛物线方程.
求两焦点的坐标分别为(-2,0),(2,0),且经过点P(2,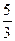 )的椭圆方程.
)的椭圆方程.
(本小题满分12分)过点M(1,1)作直线与抛物线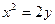 交于A、B两点,该抛物线在A、B两点处的两条切线交于点P。(I)求点P的轨迹方程;(II)求△ABP的面积的最小值。
交于A、B两点,该抛物线在A、B两点处的两条切线交于点P。(I)求点P的轨迹方程;(II)求△ABP的面积的最小值。