如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题: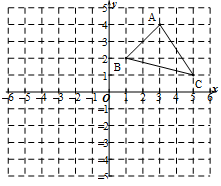
(1)△ABC的面积为
(2)画出格点△ABC(顶点均在格点上)关于x轴对称的△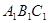
(3)指出△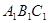 的顶点坐标.
的顶点坐标.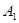 ( , ),
( , ), 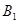 ( , ),
( , ), 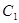 ( , )
( , )
(4)在y轴上画出点Q,使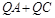 最小。
最小。
计算: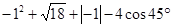 .
.
在平面直角坐标系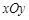 中,抛物线
中,抛物线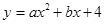 经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
求该抛物线的解析式;
若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;
该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.
如图,D是△ABC中AB边的中点,△BCE和△ACF都是等边三角形, M、N分别是CE、CF的中点.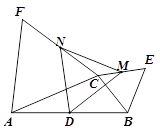
求证:△DMN是等边三角形;
连接EF,Q是EF中点,CP⊥EF于点P. 求证:DP=DQ.
同学们,如果你觉得解决本题有困难,可以阅读下面两位同学的解题思路作为参考:
小聪同学发现此题条件中有较多的中点,因此考虑构造三角形的中位线,添加出了一些辅助线;小慧同学想到要证明线段相等,可通过证明三角形全等,如何构造出相应的三角形呢?她考虑将△NCM绕顶点旋转到要证的对应线段的位置,由此猜想到了所需构造的三角形的位置.
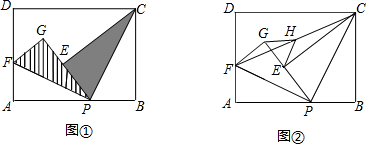
已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由.
已知二次函数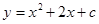 .
.当c=-3时,求出该二次函数的图象与x轴的交点坐标;
若-2<x<1时,该二次函数的图象与x轴有且只有一个交点,求c的取值范围.