（本小题满分8分）如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A（﹣2，2），B（0，5），C（0，2）．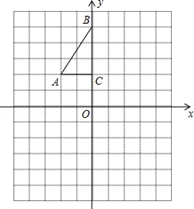
（1）将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形；
（2）平移△ABC，使点A的对应点A2坐标为（﹣2，﹣6），请画出平移后对应的△A2B2C2的图形；
（3）若将△A1B1C绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标．
某公司生产一种环保产品，需要添加一种新型原料，若每件产品的利润与新型原料价格成一次函数关系，且每件产品的利润y（元）与新型原料的价格x（元/千克）的函数图象如图：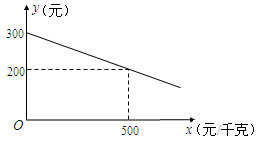
（1）当新型原料的价格为600元/千克时，每件产品的利润是多少？
（2）新型原料是一种稀少材料，为了珍惜资源，政府部门规定：新型原料每天使用量m（千克）与价格x（元/千克）的函数关系为x ="10m" +500，且m千克新型原料可生产10m件产品．那么生产300件这种产品，一共可得利润是多少？
（3）受生产能力的限制，该公司每天生产这种产品不超过450件，那么在（2）的条件下，该公司每天应生产多少件产品才能获得最大利润？最大利润是多少？
如图，一次函数
与反比例函数
的图象交于A（1,m）、B（4,n）两点．
（1）求A、B两点的坐标和反比例函数的解析式；
（2）根据图象，直接写出当y
＞y
时x的取值范围；
（3）求△AOB的面积．
如图所示，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于C（0，2），若∠ACB=90°，BC=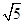
．
试求：（1）A、B两点的坐标；
（2）二次函数的表达式．
李华晚上在两站相距50m的路灯下来回散步，DF=50m．已知李华身高AB=1．7m，灯柱CD=EF=8．5m．
（1）若李华距灯柱CD的距离为DB=xm，他的影子BQ=ym，求y关于x的函数关系式．
（2）若李华在两路灯之间行走，则他前后两个影子PB+BQ是否会发生变化？请说明理由．
如图所示，一个运动员推铅球，铅球在点A处出手，出手时球离地面约2．5m．铅球落地点在B处，铅球运行中在运动员前4m处（即OC=4）达到最高点，最高点高为3m．已知铅球经过的路线是抛物线，根据图示的直角坐标系信息，请你算出该运动员的成绩．（即求OB的长度）