书正和子轩两人登一座山,书正每分钟登高10米,并且先出发30分钟,子轩每分钟登高15米,两人同时登上山顶.
(1)这座山有多高?
(2)如果将题中“书正先出发30分钟”这个条件改为“书正先爬山200米”其他条件不变,问子轩出发多少分钟追上书正?
(本小题12分)如图,有五个边长为1的小正方形组成的图形纸,我们可以把它剪开后拼成一个大正方形。
拼成的大正方形的面积与边长分别是多少?
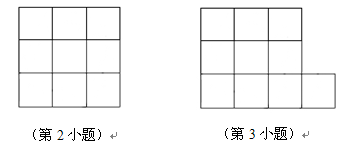
你能在下图3×3方格中,连接四个格点,组成面积为5的正方形吗?
你还能把十个小正方形组成的图形纸,剪开并拼成更大的正方形吗?若能,请在下图中画出图形,并求出它的边长是多少?
(本小题10分)我 校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
| 题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 答错人数 |
9 |
10 |
6 |
6 |
18 |
23 |
已知这n人中,平均每题有12人答错,同时第6题答错的人数恰好是第5题答错人数的2倍,且第2题有80%的同学答对。解答下面的问题:(1)总共统计了多少人?
(2)
 第5,6两题各有多少人答错?
第5,6两题各有多少人答错?(3)将统计图
 补充完整。
补充完整。
(本小题10分)求下列代数式的值(1)若a=—2,b=—3,则代数式(a+b)2—(a—b)2=___________
(2)当x—y=3时,代数式2(x—y)2+3x—3y+1=___________
(3)化简并求值:已知三个有理数
 的积是负数,其和为正数;当
的积是负数,其和为正数;当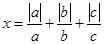 时,求代数式
时,求代数式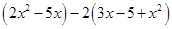 的值。
的值。
(本小题8分)出租车司机小傅某天下午营运全是在东西走向的大道上行驶的,如果规定向东为正,行车里程(单位:km)如下:
+11,-2,+3,+10,-11,+5,-15,-8(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多
 少?
少?(2)若每千米的营运额为7元,成本为1.5元/km,则这天下午他盈利多少元?
(本小题8分)解方程: ①

②
