(本小题满分12分)已知非零向量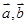 满足
满足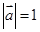 ,且
,且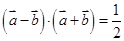 .
.
(1)求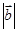 ;
;
(2)当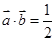 时,求向量
时,求向量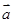 与
与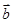 的夹角的值.
的夹角的值.
(本小题10分)如图是一个几何体的主视图和俯视图,
(1)试判断这个几何体是什么几何体;
(2)请画出它的左视图,并求该左视图的面积.
(本题12分)已知定义在区间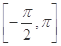 上的函数
上的函数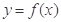 的图像关于直线
的图像关于直线 对称,当
对称,当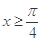 时,函数
时,函数 .
.
(1)求 的值;
的值;
(2)求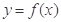 的表达式;
的表达式;
(3)若关于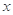 的方程
的方程 有解,那么将方程在
有解,那么将方程在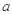 取某一确定值时所求得的所有解的和记为
取某一确定值时所求得的所有解的和记为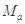 ,求
,求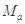 的所有可能取值及相应
的所有可能取值及相应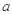 的的取值范围.
的的取值范围.
(本题12分)已知等差数列 满足:
满足: ,
, ,
, 的前n项和为
的前n项和为 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)令 (
( ),求数列
),求数列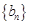 的前n项和
的前n项和 .
.
(本题12分)已知 ,
, ,
, .
.
(1)求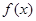 的单调递减区间;
的单调递减区间;
(2)若函数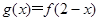 ,求当
,求当 时,
时,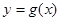 的最大值.
的最大值.