在平面直角坐标系 中,点M(
中,点M(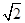 ,
,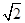 ),以点M为圆心,OM长为半径作⊙M .使⊙M与直线OM的另一交点为点B,与
),以点M为圆心,OM长为半径作⊙M .使⊙M与直线OM的另一交点为点B,与 轴、
轴、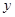 轴的另一交点分别为点D、A(如图),连接AM.点P是
轴的另一交点分别为点D、A(如图),连接AM.点P是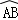 上的动点.
上的动点.

(1)∠AOB的度数为 .
(2)Q是射线OP上的点,过点Q作QC垂直于直线OM,垂足为C,直线QC交 轴于点E.
轴于点E.
①当QE与⊙M相切时,求点E的坐标;
②在①的条件下,在点P运动的整个过程中,求△ODQ面积的最大值及点Q经过的路径长.
如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA相邻的外角平分线CF于点F。
(1)求证:EO=FO
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
如下图,用长为39米的篱笆(虚线部分),一面靠墙围成矩形ABCD菜园(AB<BC,且在边BC上开一个l米宽的门.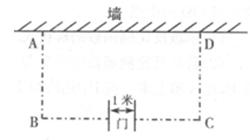
(1)要使围成的矩形ABCD菜园面积为128米2,那么矩形一边AB长应为多少米?
(2)可围成的矩形ABCD菜园的最大面积为多少平方米?此时矩形一边AB长为多少米?
如图所示,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°,CE=2BE,试判断△CDE的形状,并说明理由.
从甲学校到乙学校有 、
、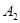 、
、 三条线路,从乙学校到丙学校有
三条线路,从乙学校到丙学校有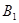 、
、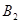 二条线路。
二条线路。
(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;
(2)小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了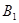 线路的概率是多少?
线路的概率是多少?
已知方程 则 ①当
则 ①当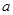 取什么值时,方程有两个不相等的实数根?②当
取什么值时,方程有两个不相等的实数根?②当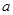 取什么值时,方程有两个相等的实数根?③、当
取什么值时,方程有两个相等的实数根?③、当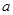 取什么值时,方程没有实数根?
取什么值时,方程没有实数根?