某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下: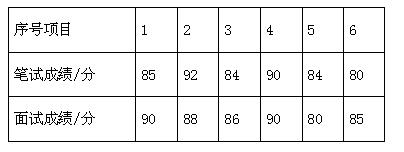
根据规定,笔试成绩和面试成绩分别按一定的百分比折算成综合成绩(综合成绩的满分仍为100分).
(1)求出这6名选手笔试成绩的中位数、众数;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.
已知:如图,△ABC中,∠ABC=∠C,BD是∠ABC的平分线,且∠BDE=∠BED,∠A=100°,求∠DEC的度数.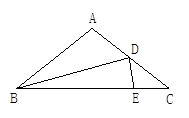
平面直角坐标系中,顺次连结(-2,1),(-2,-1),(2,-2),(2,3)各点,你会得到一个什么图形?试求出该图形的面积.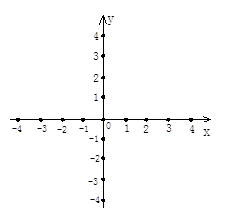
已知△ABC中,∠ACB=90°,AC=6,BC=8,过点A作直线MN⊥AC,点P是直线MN上的一个动点(与点A不重合),连结CP交AB于点D,设AP= ,AD=
,AD=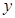 .
.如图1,若点P在射线AM上,求y与x的函数解析式;

射线AM上是否存在一点P,使以点D、A、P组成的三角形与△ABC相似,若存在,求AP的长,若不存在,说明理由;
如图2,过点B作BE⊥MN,垂足为E,以C为圆心、AC为半径的⊙C与以P为圆心PD为半径的动⊙P相切,求⊙P的半径

电瓶厂投资2000万元安装了电动自行车电瓶流水线,生产的电瓶成本为40元只,设销售单价为 元(
元(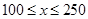 ),年销售量为
),年销售量为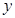 万件,年获利为
万件,年获利为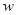 (万元).经过市场调研发现:当
(万元).经过市场调研发现:当 100元时,
100元时, 20万件.当100
20万件.当100
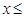 200元时,
200元时, 在100元的基础上每增加1元,
在100元的基础上每增加1元,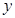 将减少0.1万件;当200
将减少0.1万件;当200
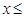 250元时,
250元时, 在200元的基础上每增加1元,
在200元的基础上每增加1元,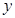 将减少0.2万件.(年获利
将减少0.2万件.(年获利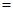 年销售额-生产成本-投资)
年销售额-生产成本-投资)当
 =180时,
=180时,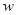 =▲万元;当
=▲万元;当 =240时,
=240时,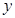 =▲万件
=▲万件求
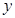 与
与 的函数关系式;
的函数关系式;当
 为何值时,第一年的年获利亏损最少?
为何值时,第一年的年获利亏损最少?
如图,一根电线杆AB和一块半圆形广告牌在太阳照射下,顶端A的影子刚好落在半圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在地面上一点E.已知BC=5米,DE=2米,半圆的直径CD=6米.
求线段EF的长
求电线杆AB的高度