在直角坐标系 中,点
中,点 到点
到点 ,
, 的距离之和是
的距离之和是 ,点
,点 的轨迹是
的轨迹是 ,直线
,直线 与轨迹
与轨迹 交于不同的两点
交于不同的两点 和
和 .
.
(1)求轨迹 的方程;
的方程;
(2)是否存在常数 ,
, ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知圆 :
: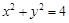 .
.
⑴直线 过点
过点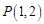 ,且与圆
,且与圆 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程;
的方程;
⑵过圆 上一动点
上一动点 作平行于
作平行于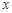 轴的直线
轴的直线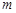 ,设
,设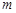 与
与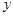 轴的交点为
轴的交点为 ,若向量
,若向量 ,求动点
,求动点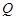 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
如图1,在直角梯形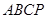 中,
中, ,
,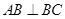 ,
,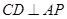 ,
,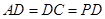 ,
,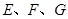 分别是
分别是 的中点,现将
的中点,现将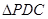 沿
沿 折起,使平面
折起,使平面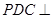 平面
平面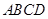 (如图2),且所得到的四棱锥
(如图2),且所得到的四棱锥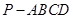 的正视图、侧视图、俯视图的面积总和为8.
的正视图、侧视图、俯视图的面积总和为8.
⑴求点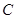 到平面
到平面 的距离;
的距离;
⑵求二面角 的大小的夹角的余弦值;
的大小的夹角的余弦值;
⑶在线段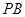 上确定一点
上确定一点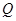 ,使
,使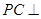 平面
平面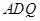 ,并给出证明过程.
,并给出证明过程.
设命题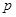 :函数
:函数 在
在 上单调递增;命题
上单调递增;命题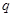 :不等式
:不等式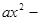
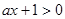 对任意的
对任意的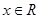 恒成立.若“
恒成立.若“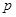 且
且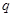 ”为假,“
”为假,“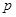 或
或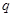 ”为真,求
”为真,求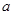 的取值范围.
的取值范围.
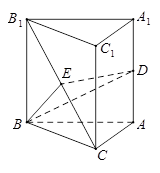
如图,在棱长都相等的正三棱柱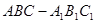 中,
中,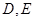 分别为
分别为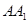 ,
,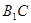 的中点.
的中点.
⑴求证: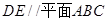 ;
;
⑵求证: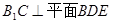 .
.
椭圆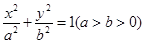 的两个焦点及其与坐标轴的一个交点正好是一个等边三角形的三个顶点,且椭圆上的点到焦点距离的最小值为
的两个焦点及其与坐标轴的一个交点正好是一个等边三角形的三个顶点,且椭圆上的点到焦点距离的最小值为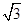 ,求椭圆的方程.
,求椭圆的方程.