[2014高考真题] 已知等差数列{an}满足:a1=2,且a1,a2,a5成等比数列.
(1)求数列{an}的通项公式.
(2)记Sn为数列{an}的前n项和,是否存在正整数n,使得Sn>60n+800?若存在,求n的最小值;若不存在,说明理由.
已知函数
(1)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(2)设 的内角A、B、C的对边分别为
的内角A、B、C的对边分别为 ,且
,且 ,若向量
,若向量 与向量
与向量 共线,求
共线,求 的值。
的值。
(本小题满分12分)若对于正整数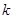 、
、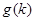 表示
表示
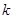 的最大奇数因数,
的最大奇数因数, 例如
例如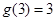 ,
,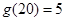 ,并且
,并且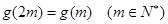 ,设
,设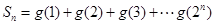
(1)求S1、S2、S3;
(2)求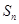 ;
;
(3)设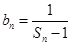 ,求证数列
,求证数列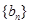 的前
的前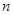 顶和
顶和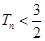 .
.
(本小题满分12分)中心在原点,焦点在x轴上的椭圆C上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆C的方程;
(2)若直线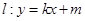 与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求该定点的坐标.
与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求该定点的坐标.
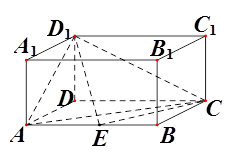
(本小题满分12分)在如图的长方体中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)当E为AB的中点时,求点E到平面ACD1的距离;
(2)AE等于何值时,二面 角D1-EC-D的大小为
角D1-EC-D的大小为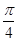 .
.
(本小题满分12分)已知双曲线 的左、右顶点分别为
的左、右顶点分别为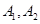 ,点
,点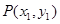 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.
(1)求直线 与
与 交点的轨迹E的方程
交点的轨迹E的方程
(2)若过点H(0, h)(h>1)的两条直线 和
和 与轨迹E
与轨迹E 都只有一个公共点,且
都只有一个公共点,且 ,求
,求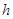 的值.
的值.