(本小题满分15分)今年的国庆假期是实施免收小型客车高速通行费后的第一个重大节假日,有一个自驾游车队。该车队是由31辆车身长都约为5m(以5m计算)的同一车型组成的,行程中经过一个长为2725m的隧道(通过该隧道的车速不能超过25m/s),若车队匀速通过该隧道,设车队的速度为 m/s ,根据安全和车流的需要,当
m/s ,根据安全和车流的需要,当 时,相邻两车之间保持20m的距离;当
时,相邻两车之间保持20m的距离;当 时,相邻两车之间保持
时,相邻两车之间保持 m的距离.自第1辆车车头进入隧道至第31辆车车尾离开隧道所用的时间为
m的距离.自第1辆车车头进入隧道至第31辆车车尾离开隧道所用的时间为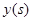 .
.
(1)将 表示为
表示为 的函数;
的函数;
(2)求该车队通过隧道时间 的最小值及此时车队的速度.
的最小值及此时车队的速度.
(本小题满分13分)
随机调查某社区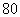 个人,以研究这一社区居民在
个人,以研究这一社区居民在 时间段的休闲方
时间段的休闲方
式与性别的关系,得到下面的数据表:
| 休闲方式 性别 |
看电视 |
看书 |
合计 |
| 男 |
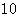 |
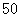 |
 |
| 女 |
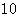 |
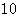 |
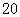 |
| 合计 |
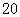 |
 |
 |
(1)将此样本的频率估计为总体的概率,随机调查 名在该社区的男性,设调查的
名在该社区的男性,设调查的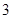 人
人
在这一时间段以看书为休闲方式的人数为随机变量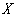 ,求
,求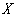 的分布列和期望;
的分布列和期望;
(2)根据以上数据,能否有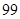 %的把握认为“在
%的把握认为“在 时间段的休闲方式与
时间段的休闲方式与
性别有关系”?
参考公式: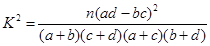 ,其中
,其中 .
.
参考数据:
 |
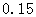 |
 |
 |
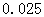 |
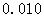 |
 |
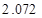 |
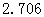 |
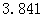 |
 |
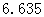 |
(本小题满分12分)
已知函数 ,
, (其中
(其中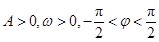 ),其部分图
),其部分图
像如图5所示.
(1)求函数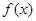 的解析式;
的解析式;
(2)已知横坐标分别为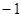 、
、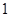 、
、 的三点
的三点 、
、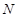 、
、 都在函数
都在函数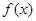 的图像上,求
的图像上,求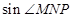 的值.
的值.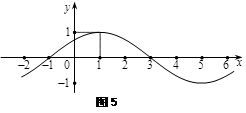
(几何证明选讲选做题)如图4, 是圆
是圆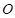 上的两点,且
上的两点,且 ,
, ,
, 为
为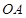 的中点,连接
的中点,连接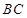 并延长交圆
并延长交圆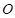 于点
于点 ,则
,则 .
.
已知等比数列 的首项
的首项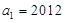 ,公比
,公比 ,数列
,数列 前n项和记为
前n项和记为 ,前n
,前n
项积记为 .
.
(Ⅰ)求数列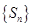 的最大项和最小项;
的最大项和最小项;
(Ⅱ)判断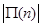 与
与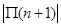 的大小, 并求
的大小, 并求 为何值时,
为何值时, 取得最大值;
取得最大值;
(Ⅲ)证明 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这
中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这
些等差数列的公差按从小到大的顺序依次设为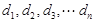 ,证明:数列
,证明:数列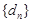 为等比数列。
为等比数列。
(参考数据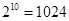 )
)
(本小题满分14分) 已知函数 ,且函数
,且函数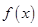 是
是 上的增函数。
上的增函数。
(1)求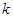 的取值范围;
的取值范围;
(2)若对任意的 ,都有
,都有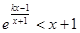 (e是自然对数的底),求满足条件的最大整数
(e是自然对数的底),求满足条件的最大整数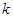
的值。