(本小题8分)书架上有10本不同的书,其中语文书4本,数学书3本,英语书3本,现从中取出3本书.求:
( 1 )3本书中至少有1本是数学书的概率;
( 2 ) 3本书不全是同科目书的概率.
3本书不全是同科目书的概率.
解:(1)3本书中至少有 1本是数学书的概率为
1本是数学书的概率为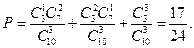
 (4分)
(4分)
或解  (4分)
(4分)
(2)事件“3本书不全是同科目书”的对立事件是事件“3本书是同科目书”,
而事件“3本书是同科目书”的概率为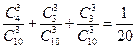 (7分
(7分
∴3本书不全是同科目书的概率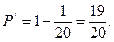
. (1)求过原点且与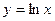 相切的切线方程?
相切的切线方程?
(2)若命题
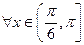 ;
;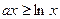 .命题
.命题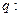
 ;
;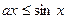 .
.
求 为真命题时,
为真命题时,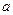 的取值范围?
的取值范围?
.已知:椭圆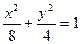 的左右焦点为
的左右焦点为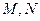 ;直线
;直线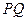 经过
经过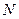 交椭圆于
交椭圆于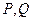 两点.
两点.
(1)求证: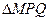 的周长为定值.
的周长为定值.
(2)求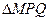 的面积的最大值?
的面积的最大值?
.过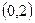 点作斜率为
点作斜率为 的直线
的直线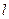 与双曲线
与双曲线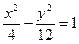 有两个不同交点
有两个不同交点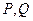 .
.
⑴求 的取值范围?
的取值范围?
⑵是否存在斜率 ,使得向量
,使得向量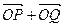 与双曲线的一条渐近线的方向向量平行.若存在,求出
与双曲线的一条渐近线的方向向量平行.若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
.如图,等边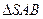 与直角梯形ABCD垂直,
与直角梯形ABCD垂直,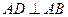 ,
,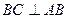 ,
,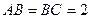 ,
,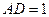 .若E,F分别为AB,CD的中点.
.若E,F分别为AB,CD的中点.
(1)求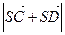 的取值?
的取值?
(2)求面SCD与面SAB所成的二面角大小?