（本小题满分12分）定义在
上的函数
，如果满足：对任意
，存在常数
，都有
成立，则称
是上的有界函数，其中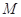
称为函数的上界.已知函数
，
（1）当
时，求函数
在
上的值域，并判断函数在上是否为有界函数，请说明理由；
（2）若函数在
上是以4为上界的有界函数，求实数
的取值范围.
已知数列 {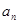
}中，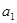
=" 8" ，
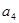=" 2" ，且满足
.
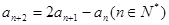(1)求数列 {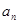}的 通项公式；
（2）设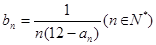
,
= 
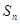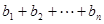，是否存在最大的整数m ,使得对任意的
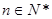，都有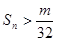
成立？若存在，求出m的值；若不存在，请说明理由 .
设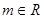
,解关于x的不等式
.
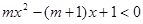已知数列{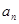
}是公差不为零的等差数列，
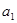=" 1" ，且，
，
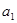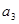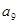成等比数列.
(1)求数列{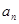}的通项公式 ；
(2)求数列{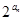
}的前n项和
.
（1）设a > 0 , b > 0 ,求证: 
a + b ;
（2）设x,y都是正实数 ,且x + y =" 1" ，求证：(1+ 
)(1+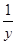 
) ≥ 9 .
如图，AB是半圆的直径，C是AB延长线上一点，CD切半圆于点D，CD=2，
,垂足为E,且E是OB的中点，求BC的长。