（本小题满分12分）某校高三文科分为四个班．高三数学调研测试后， 随机地在各班抽取部分学生进行测试成绩统计，各班被抽取的学生人数恰好成等差数列，人数最少的班被抽取了22人．抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示，其中120～130（包括120分但不包括130分）的频率为0．05，此分数段的人数为5人．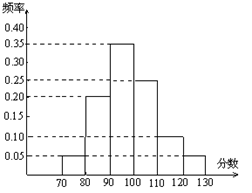
（1）问各班被抽取的学生人数各为多少人?
（2）求平均成绩；
（3）在抽取的所有学生中，任取一名学生，
求分数不小于90分的概率．
抛物线的标准方程。
上一点
，它到左准线的距离为
，求点
上任何一点到两条渐近线的距离之积为定值．
的一底边
在平面
内，另一底边
在平面
到平面
，若
，求
到平面
的左、右两个焦点分别为
，点
在双曲线上，且
，求
的面积．