(本小题满分12分)银川市有甲,乙两家室内羽毛球馆,两家设备和服务都相当,但收费方式不同.甲羽毛球馆每小时50元;乙羽毛球馆按月计费,一个月中30小时以内(含30小时)900元,超过30小时的部分每小时20元.肖老师为了锻炼身体,准备下个月从这两家羽毛球馆中选择一家进行健身活动,其活动时间不少于15小时,也不超过40小时.设甲羽毛球馆健身 小时的收费为
小时的收费为 元,乙羽毛球馆健身
元,乙羽毛球馆健身 小时的收费为
小时的收费为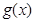 元.
元.
(Ⅰ)当 时,分别写出函数
时,分别写出函数 和
和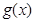 的表达式;
的表达式;
(Ⅱ)请问肖老师选择哪家羽毛球馆健身比较合算?为什么?
已知数列 满足:
满足: ,其中
,其中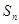 为
为 的前n项和.
的前n项和.
(1)求 的通项公式;
的通项公式;
(2)若数列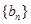 满足
满足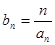 ,求
,求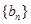 的前n项和
的前n项和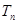 .
.
已知条件p: 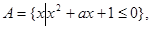 条件q:
条件q: 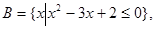 若
若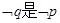 的充分但不必要条件,求实数
的充分但不必要条件,求实数 的取值范围.
的取值范围.
已知 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且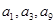 成等比数列.
成等比数列.
(1)求数列 的通项;
的通项;
(2)记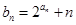 ,求数列
,求数列 的前
的前 项和
项和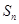
(本小题满分12分)
已知椭圆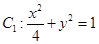 ,椭圆
,椭圆 以
以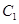 的长轴为短轴,且与
的长轴为短轴,且与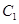 有相同的离心率.
有相同的离心率.
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点,点A,B分别在椭圆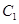 和
和 上,
上,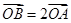 ,求直线
,求直线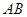 的方程.
的方程.
.(本小题满分12分)
已知函数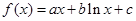 ,
,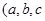 是常数)在x=e处的切线方程为
是常数)在x=e处的切线方程为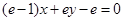 ,
, 既是函数
既是函数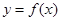 的零点,又是它的极值点.
的零点,又是它的极值点.
(1)求常数a,b,c的值;
(2)若函数 在区间(1,3)内不是单调函数,求实数m的取值范围;
在区间(1,3)内不是单调函数,求实数m的取值范围;
(3)求函数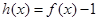 的单调递减区间,并证明:
的单调递减区间,并证明: