(本小题满分12分)已知向量 ,向量
,向量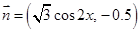 ,函数
,函数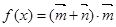 .
.
(Ⅰ)求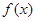 的最小正周期
的最小正周期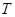 ;
;
(Ⅱ)已知 分别为
分别为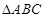 内角
内角 的对边,
的对边,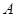 为锐角,
为锐角,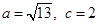 ,且
,且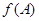 恰是
恰是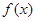 在
在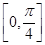 上的最大值,求
上的最大值,求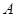 和
和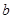 .
.
对于在区间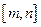 上有意义的两个函数
上有意义的两个函数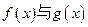 ,如果对任意
,如果对任意 均有
均有 ,则称
,则称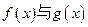 在
在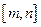 上是接近的,否则称
上是接近的,否则称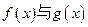 在
在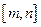 上是非接近的,现有两个函数
上是非接近的,现有两个函数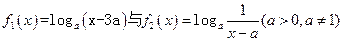 ,给定区间
,给定区间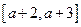 .
.
(1)若 在给定区间
在给定区间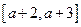 上都有意义,求
上都有意义,求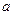 的取值范围;
的取值范围;
(2)讨论 在给定区间
在给定区间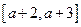 上是否是接近的?
上是否是接近的?
已知二次函数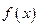 满足
满足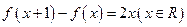 ,且
,且 。
。
(1)求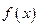 的解析式;
的解析式;
(2)当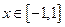 时,不等
时,不等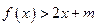 式恒成立,求实数
式恒成立,求实数 的取值范围;
的取值范围;
(3)设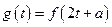 ,
,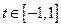 ,求
,求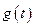 的最大值。
的最大值。
已知 为都大于1的不全相等的正实数,
为都大于1的不全相等的正实数,
求证:
已知关于 的方程
的方程 有实数根
有实数根 (1)求实数
(1)求实数 的值
的值
(2)若复数 满足
满足 ,求
,求 为何值时,
为何值时, 有最小值,并求出
有最小值,并求出 的值。
的值。
学校为了调查喜欢语文学科与性别是否有关系,随机调查了50名学生,男生中有12人不喜欢语文,有10人喜欢语文,女生中有8人不喜欢语文,有20人喜欢语文,根据所给数据,
(1)写出 列联表;
列联表;
(2)由 ,及临界值3.841和6.635作统计分析推断。
,及临界值3.841和6.635作统计分析推断。