（本小题满分14分）已知函数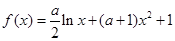
．
（Ⅰ）当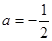
时，求
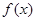在区间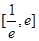
上的最小值；
（Ⅱ）讨论函数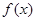的单调性；
（Ⅲ）当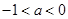
时，有
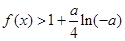恒成立，求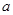
的取值范围．
（本小题满分13分）
设函数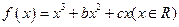
，已知
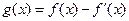是奇函数.
（Ⅰ）求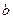
、
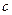的值;（Ⅱ）求
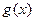的单调区间与极值.
（本小题满分13分）
已知
的展开式中第五项的系数与第三项的系数的比是10:1
（1）求展开式中各项系数的和；
（2）求展开式中含
的项；
（本小题满分13分）
4位学生与2位教师并坐合影留念，针对下列各种坐法，试问：各有多少种不同的坐法？（用数字做答）
（1）教师必须坐在中间；
（2）教师不能坐在两端，但要坐在一起；
（3）教师不能坐在两端，且不能相邻．
已知函数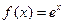
（
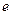为自然对数的底数），
（
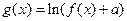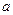为常数），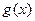
是实数集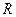
上的奇函数．
（1）求证：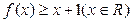
；
（2）讨论关于
的方程：
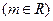的根的个数；
（3）设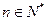
，证明：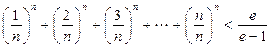
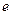（为自然对数的底数）．
已知平面上两定点C（
1,0）,D（1，0）和一定直线
，
为该平面上一动点，作
，垂足为Q，且
（1）问点在什么曲线上，并求出曲线的轨迹方程M；
（2）又已知点A为抛物线
上一点，直线DA与曲线M的交点
B不在
轴的右侧，且点B不在
轴上，并满足
的最小值．