(本小题满分13分) 已知椭圆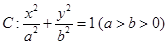 经过点
经过点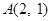 ,离心率为
,离心率为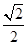 ,过点
,过点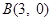 的直线
的直线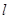 与椭圆
与椭圆 交于不同的两点
交于不同的两点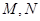 .
.
(1)求椭圆 的方程;
的方程;
(2)求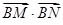 的取值范围.
的取值范围.
设平面向量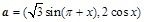 ,
, ,已知函数
,已知函数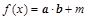 在
在 上的最大值为6.
上的最大值为6.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若 ,
,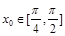 .求
.求 的值.
的值.
已知函数 ,其中
,其中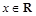 ,
, .
.
(Ⅰ)若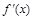 的最小值为
的最小值为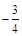 ,试判断函数
,试判断函数 的零点个数,并说明理由;
的零点个数,并说明理由;
(Ⅱ)若函数 的极小值大于零,求
的极小值大于零,求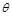 的取值范围.
的取值范围.
设等差数列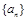 的前n项和为
的前n项和为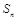 ,且
,且 ,
, .
.
(Ⅰ)求数列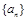 的通项公式;
的通项公式;
(Ⅱ)设数列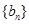 前n项和为
前n项和为 ,且
,且 ,令
,令 .求数列
.求数列 的前n项和
的前n项和 .
.
在△ABC中,角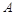 、
、 、
、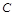 的对边分别为
的对边分别为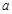 、
、 、
、 ,设S为△ABC的面积,满足
,设S为△ABC的面积,满足 .
.
(Ⅰ)求角C的大小;
(Ⅱ)若 ,且
,且 ,求
,求 的值.
的值.
在一次数学统考后,某班随机抽取10名同学的成绩进行样本分析,获得成绩数据的茎叶图如下.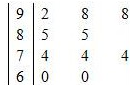
(Ⅰ)计算样本的平均成绩及方差;
(Ⅱ)现从80分以上的样本中随机抽出2名学生,求抽出的2名学生的成绩分别在 、
、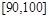 上的概率.
上的概率.