(本小题满分12分)在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点. 
(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)当平面PCD与平面ABCD成多大角时,直线EF⊥平面PCD?
已知抛物线和椭圆都经过点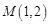 ,它们在
,它们在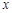 轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点.
(1)求这两条曲线的方程;
(2)对于抛物线上任意一点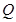 ,点
,点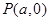 都满足
都满足 ,求
,求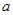 的取值范围.
的取值范围.
已知函数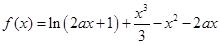
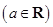 .
.
(1)若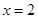 为
为 的极值点,求实数
的极值点,求实数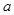 的值;
的值;
(2)当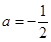 时,方程
时,方程 有实根,求实数
有实根,求实数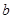 的最大值。
的最大值。
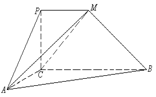
如图,四边形PCBM是直角梯形,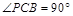 ,
,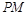 ∥
∥ ,
,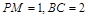 .又
.又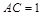 ,
,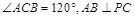 ,直线AM与直线PC所成的角为
,直线AM与直线PC所成的角为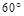 .
.
(1)求证: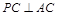 ;
;
(2)求二面角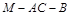 的余弦值.
的余弦值.
现有长分别为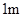 、
、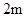 、
、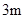 的钢管各
的钢管各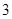 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取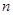 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的,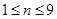 ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.
(1)当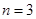 时,记事件
时,记事件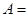 {抽取的
{抽取的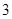 根钢管中恰有
根钢管中恰有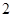 根长度相等},求
根长度相等},求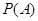 ;
;
(2)当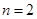 时,若用
时,若用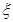 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求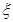 的分布列;
的分布列;
②令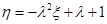 ,
, ,求实数
,求实数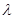 的取值范围.
的取值范围.
如图,在△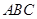 中,
中,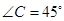 ,
, 为
为 中点,
中点, .记锐角
.记锐角 .且满足
.且满足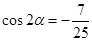 .
.
(1)求 ;
;
(2)求 边上高的值.
边上高的值.