(本小题满分10分)【选修4-4:坐标系与参数方程】
已知曲线C的极坐标方程为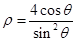 ,以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,直线
,以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,直线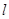 的参数方程为
的参数方程为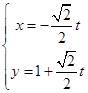 (t为参数).
(t为参数).
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程,把直线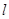 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)求直线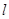 被曲线C截得的线段AB的长.
被曲线C截得的线段AB的长.
如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.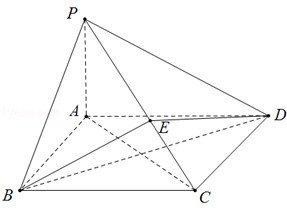
(1)证明:BD⊥平面PAC;
(2)若PA=1,AD=2,求二面角B﹣PC﹣A的正切值.
已知函数f(x)=2sin( x﹣
x﹣ ),x∈R.
),x∈R.
(1)求f(0)的值;
(2)设α,β∈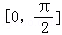 ,f(3
,f(3 )=
)=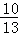 ,f(3β+
,f(3β+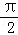 )=
)= .求sin(α+β)的值.
.求sin(α+β)的值.
已知函数 (
( 为常数)的图像与
为常数)的图像与 轴交于点
轴交于点 ,曲线
,曲线 在点
在点 处的切线斜率为
处的切线斜率为 .
.
(1)求 的值及函数
的值及函数 的极值;
的极值;
(2)证明:当 时,
时, ;
;
(3)证明:对任意给定的正数 ,总存在
,总存在 ,使得当
,使得当 时,恒有
时,恒有
已知函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)将函数 的图象向右平移
的图象向右平移 个单位长度,再向下平移
个单位长度,再向下平移 (
( )个单位长度后得到函数
)个单位长度后得到函数 的图象,且函数
的图象,且函数 的最大值为2.
的最大值为2.
(ⅰ)求函数 的解析式;
的解析式;
(ⅱ)证明:存在无穷多个互不相同的正整数 ,使得
,使得 .
.
已知曲线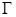 上的点到点
上的点到点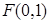 的距离比它到直线
的距离比它到直线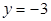 的距离小2.
的距离小2.
(1)求曲线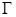 的方程;
的方程;
(2)曲线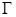 在点
在点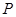 处的切线
处的切线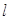 与
与 轴交于点
轴交于点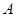 .直线
.直线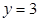 分别与直线
分别与直线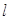 及
及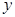 轴交于点
轴交于点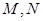 ,以
,以 为直径作圆
为直径作圆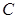 ,过点
,过点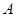 作圆
作圆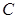 的切线,切点为
的切线,切点为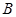 ,试探究:当点
,试探究:当点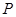 在曲线
在曲线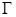 上运动(点
上运动(点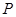 与原点不重合)时,线段
与原点不重合)时,线段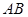 的长度是否发生变化?证明你的结论.
的长度是否发生变化?证明你的结论.