如图,描述了小明早晨8时到下午14时,骑摩托车从甲地到乙地所走路程与时间的关系,根据折线图提供的信息思考下列问题:
(1)到12时,此人共走了多少千米?
(2)从甲地到乙地途中休息了几次,从几时到几时?
(3)此人前进的最快速度是多少千米每小时?
解下列方程:(每题4分,共8分)
(1)x2-2x=-1;(2)(x+3)2=2x(x+3).
已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.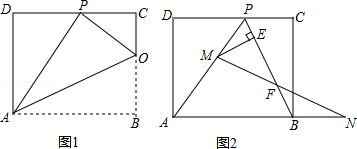
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;(提示:直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角为300)
(3)如图2,

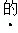


 ,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
如图1,在平面直角坐标系中,点M在x轴的正半轴上,⊙M交x轴 于A、B两点,交y轴C、D于两点,且C为弧AE的中点,AE交y轴于点G,若A点的坐标为(-2,0),CD=8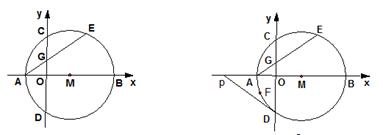
(1)求⊙M的半径
(2)求AE的长
(3)如图2,过点D作⊙M的切线,交x轴于点P.动点F在⊙M圆周上运动时, 的比值是否发生变化,若不变,求出比值:若不变,请说明变化规律
的比值是否发生变化,若不变,求出比值:若不变,请说明变化规律
甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一
些物体进行了测量.下面是他们通过测量得到的一些信息:
甲组:如图(1),测得一根直立于平地,长为80cm的竹竿的影长为60cm.
乙组:如图(2),测得学校旗杆的影长为900cm.
丙组:如图(3),测得校园景灯的灯罩部分影长HQ为90cm,灯杆被阳光照射到的部分PG长40cm,未被照射到的部分KP长24cm.(灯罩视为圆柱体,灯杆粗细忽略不计且穿过灯罩中轴线)
(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度是多少米;
(2)请根据甲、丙两组得到的信息,求:①灯罩底面半径MK的长; ②灯罩的高度KK’的长.
如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
(1)当PE⊥AB,PF⊥BC时,如图1,则 的值为;
的值为;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;
的值;