A,B两地相距18公里,甲工程队要在A,B两地间铺设一条输送天然气管道,乙工程队要在A,B两地间铺设一条输油管道.已知甲工程队每周比乙工程队少铺设1公里,甲工程队提前3周开工,结果两队同时完成任务,求甲、乙两工程队每周各铺设多少公里管道?
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中:
(1)A→C( , ),B→D( , );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+1,-1),(-2,+3),(-1,-2),请在图中标出P的位置.
在某次抗险救灾中,消防官兵的冲锋舟沿东西方向的河流营救灾民,早晨从A地出发,晚上到达B地,约定向东为正方向,当天的航行路程记录如下(单位:km):+14,-9,+8,-7,+13,-6,+10,-5.
(1)通过计算说明:B地在A地的什么方向,与A地相距多远?
(2)救灾过程中,最远处离出发点A有多远?
(3)若冲锋舟每千米耗油0.5 L,油箱容量为29L,求途中还需补充多少升油.
(1)请你把有理数: 、+(-2)、5.2、
、+(-2)、5.2、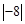 、25%、
、25%、 、
、 、0按照下列标准进行分类.
、0按照下列标准进行分类.
正分数:{ };
整数:{ };
负有理数:{ }.
(2)你会“二十四点”一游戏吗?请你在(1)的有理数中选取其中四个,运用“二十四点”游戏规则,列出一个算式,并验证其结果等于24.
已知多项式:A= ,B=
,B= .
.
(1)当 ,
,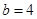 时,求3A-6B的值;
时,求3A-6B的值;
(2)若多项式C满足:C=A-2B-C,试用a、b的代数式表示C.
(本题共3小题,每小题4分,满分12分)先化简,后求值:
(1)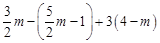 ,其中
,其中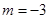 .
.
(2)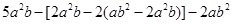 ,其中
,其中 ,
,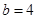 .
.
(3)如果代数式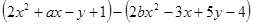 的值与字母x所取的值无关,试求代数式
的值与字母x所取的值无关,试求代数式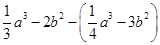 的值.
的值.