在某次抗险救灾中，消防官兵的冲锋舟沿东西方向的河流营救灾民，早晨从A地出发，晚上到达B地，约定向东为正方向，当天的航行路程记录如下（单位：km）：＋14，－9，＋8，－7，＋13，－6，＋10，－5．
（1）通过计算说明：B地在A地的什么方向，与A地相距多远？
（2）救灾过程中，最远处离出发点A有多远？
（3）若冲锋舟每千米耗油0.5 L，油箱容量为29L，求途中还需补充多少升油．
如图所示，在矩形ABCD中，DE⊥AC于点E，设∠ADE＝α，且cosα＝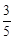
，AB＝4，则AC的长为多少？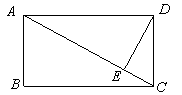 
抛物线y=-x2+bx+c经过点A、B、C，已知A（-1，0），C（0，3）．
（1）求抛物线的解析式；
（2）如图1，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，当△BDC的面积最大时，求点P的坐标；
（3）如图2，抛物线顶点为E，EF⊥x轴于F点，M（m，0）是x轴上一动点，N是线段EF上一点，若∠MNC=90°，请指出实数m的变化范围，并说明理由．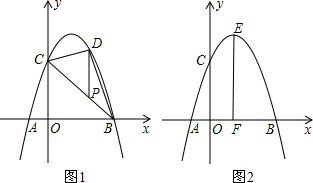
如图1，⊙O是△ABC的外接圆，AB是直径，OD∥AC，且∠CBD=∠BAC，OD交⊙O于点E．
（1）求证：BD是⊙O的切线；
（2）若点E为线段OD的中点，证明：以O、A、C、E为顶点的四边形是菱形；
（3）作CF⊥AB于点F，连接AD交CF于点G（如图2），求FG FC 的值．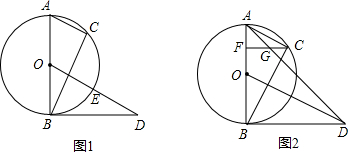
某工厂计划生产A、B两种产品共50件，需购买甲、乙两种材料．生产一件A产品需甲种材料30千克、乙种材料10千克；生产一件B产品需甲、乙两种材料各20千克．经测算，购买甲、乙两种材料各1千克共需资金40元，购买甲种材料2千克和乙种材料3千克共需资金105元．
（1）甲、乙两种材料每千克分别是多少元？
（2）现工厂用于购买甲、乙两种材料的资金不超过38000元，且生产B产品不少于28件，问符合条件的生产方案有哪几种？
（3）在（2）的条件下，若生产一件A产品需加工费200元，生产一件B产品需加工费300元，应选择哪种生产方案，使生产这50件产品的成本最低？（成本=材料费+加工费）
阅读材料：
例：说明代数式 x2+1 + (x-3)2+4 的几何意义，并求它的最小值．
解： x2+1 + (x-3)2+4 =" (x-0)2+12" + (x-3)2+22 ，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则 (x-0)2+12 可以看成点P与点A（0，1）的距离， (x-3)2+22 可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA+PB的最小值．
设点A关于x轴的对称点为A′，则PA=PA′，因此，求PA+PB的最小值，只需求PA′+PB的最小值，而点A′、B间的直线段距离最短，所以PA′+PB的最小值为线段A′B的长度．为此，构造直角三角形A′CB，因为A′C=3，CB=3，所以A′B="3" 2 ，即原式的最小值为3 2 ．
根据以上阅读材料，解答下列问题：
（1）代数式 (x-1)2+1 + (x-2)2+9 的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B （2，3）的距离之和．（填写点B的坐标）
（2）代数式 x2+49 + x2-12x+37 的最小值为．